Глава 4. Второй закон.
4.1. Определение.
Каждая термодинамическая система обладает функцией состояния -энтропией. Энтропия прцесса вычисляется следующим образом. Система переводится из начального состояния в соответствующее конечное состояние через последовательность состояний равновесия, вычисляются все подводимые при этом к системе порции тепла dQ, делятся каждая на соответствующую ей абсолютную температуру Т источника теплоты и все полученные таким образом значения суммируются
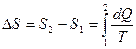
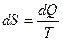
При реальных (не идеальных) процессах энтропия замкнутой (изолированной) системы возрастает
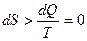 , т.е.
, т.е. 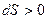
Энтропия – способность к превращению (Клаузиус)
По I закону 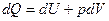 и для идеального газа
и для идеального газа
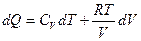
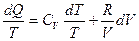
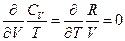 т.е. для идеального газа
т.е. для идеального газа 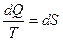 обладает свойствами полного дифференциала, т.е. S есть функция состояния.
обладает свойствами полного дифференциала, т.е. S есть функция состояния.
Распространение 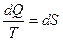 на все системы и есть II закон на все системы и есть II закон
|
4.2. Другие формулировки
Тепло не может само по себе перейти от системы с меньшей температурой к системе с большей температурой (Клаузиус).
Невозможно получать работу, только охлаждая отдельное тело ниже температуры самой холодной части окружающей среды (Кельвин).
4.3. Обратимые и необратимые процессы.
Процесс называется равновесным, если в прямом и обратном направлении проходит через одни и те же состояния бесконечно близкие к равновесию. Работа равновесного процесса имеет максимальную величину по сравнению с неравновесными процессами и называется максимальной работой.
Если равновесный процесс протекает в прямом, а затем в обратном направлении так, что не только система, но и окружающая среда возвращается в исходное состояние и в результате процесса не остается никаких изменений во всех участвовавших в процессе телах, то процесс называется обратимым.
Обратимый процесс – такая же абстракция, что и идеальный газ.
Крайние случаи необратимых процессов : переход энергии от горячего тела к холодному в форме теплоты при конечной разнице температур, переход механической работы в теплоту при трении, расширение газа в пустоту, диффузия, взрывные процессы, растворение в ненасыщенном растворе.
Эти необратимые процессы идут самопроизвольно без воздействия извне и приближают систему к равновесию.
4.4. Изменение энтропии в различных процессах
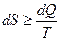
причем знак = относится к обратимым процессам, а знак > к необратимым.
Если требуется вычислить энтропию необратимого процесса необходимо провести обратимый процесс между теми же самыми конечным и начальным состоянием (используем тот факт, что энтропия – функция состояния).
а) Изотермический процесс
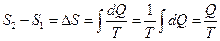 Q –часто это скрытая теплота
Q –часто это скрытая теплота
фазовых переходов.
б) Изменение температуры при 
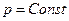


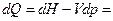
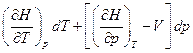 , следовательно
, следовательно  , т.к.
, т.к. 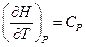
Энтропия необратимого процесса
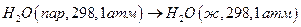
Теплота конденсации при 298 К равна – 10519 кал
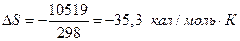
Ответ, очевидно, не верен, поскольку процесс необратимый. Проведем его обратимо :

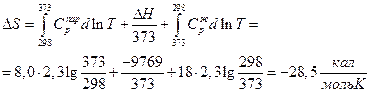
( -9769 – теплота конденсации при 373 К)
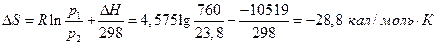
Заметим, что действительно
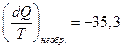 меньше, чем
меньше, чем 
4.5. Закон Джоуля
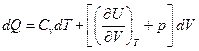
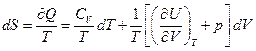 это полный дифференциал, следовательно
это полный дифференциал, следовательно 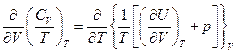
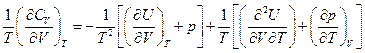
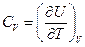
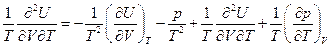
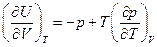
Для идеального газа 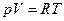
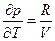 и
и
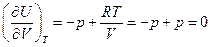
Для любых систем 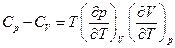
Для газа Ван-дер-Ваальса 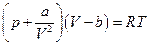 и
и 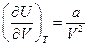
4.6. Постулат Планка. Абсолютная энтропия.
Зададимся вопросом, каково изменение энтропии некоего процесса, который протекает при температуре около абсолютного нуля. Например, имеем две кристаллические модификации металлического олова: низкотемпературную, α - Sn, и высокотемпературную – обычное белое олово, β – Sn. Они находятся в равновесии при 14 0С (287 К), теплота равновесного превращения 497 кал/моль, а энтропия его 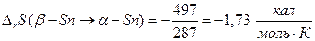
Дата добавления: 2015-07-30; просмотров: 1072;
