Если в наличии конечное изменение состояния, то имеем конечный процесс 1 → 2
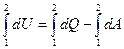 (2)
(2)

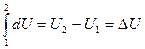


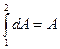
(2) превращается в 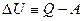 (3)
(3)
U, Q и А имеют одинаковую размерность.
2.4. Работа расширения.
Пусть наша система характеризуется только одним внешним параметром объемом V. Давление Рхарактеризует взаимодействие системы с внешней средой и измеряется силой, отнесенной к единице поверхности. Если система находится в равновесии, то давление одинаково во всех частях системы и равняется внешнему давлению. Тогда работа изменения объема системы


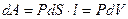
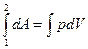
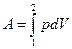 зависит от р=р(V)
зависит от р=р(V)
V = Const dV = 0 dA=0 A=0,
т.е. ΔU = 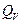
в этом случае тепловой эффект 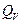 равен изменению функции состояния.
равен изменению функции состояния.
p = Const 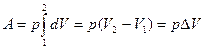
T = Const 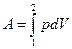 В этом случае необходимо знать уравнение состояния системы
В этом случае необходимо знать уравнение состояния системы 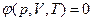 .
.
Если система - идеальный газ, то 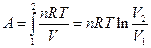 ,
,
поскольку pV = nRT, А 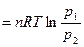 в связи с тем, что при T=const p1V1 = p2V2
в связи с тем, что при T=const p1V1 = p2V2
R=0,082 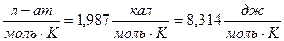 Это стоит запомнить.
Это стоит запомнить.
Кроме того при Т = Const для идеального газа U = Const, dU = 0, A = Q т.е. все тепло, полученное идеальным газом, перешло в работу.
Для адиабатического процесса dQ = 0 (Q = 0)
dU = -dA -ΔU = A
т.е. положительная работа совершается за счет уменьшения U.
2.5. Теплота и теплоемкость
Теплоемкостью системы называется отношение количества тепла, сообщенного системе в каком-либо процессе, к соответствующему изменению температуры
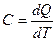 1 кал = 4,1840 дж, 1 дж = 107 эрг (СИ)
1 кал = 4,1840 дж, 1 дж = 107 эрг (СИ)
Поскольку Q -функция процесса, то
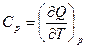 , а
, а 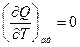 ,
, 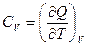
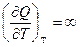
Связь между Ср и Сv для любых систем найдем следующим образом.
dQ = dU + pdV (I закон)
Выберем в качестве независимых переменных объем и температуру, тогда внутренняя энергия
 и
и 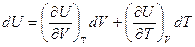
а 
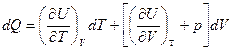
Разделим правую и левую части на dT, получим
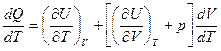
Отношение 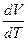 есть отношение приращений независимых переменных, то-есть величина неопределенная, и чтобы снять неопределенность, необходимо указать характер процесса. Пусть процесс изохорный.
есть отношение приращений независимых переменных, то-есть величина неопределенная, и чтобы снять неопределенность, необходимо указать характер процесса. Пусть процесс изохорный.
V = Const 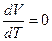 и
и 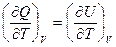 =СV
=СV
Отсюда 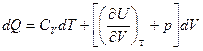
Далее при p = Const 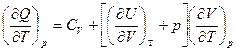 = Ср
= Ср
И для любых систем 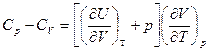

Для идеальных газов
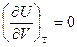 (Строго докажем при II законе).
(Строго докажем при II законе).
а поскольку pV = RT, то
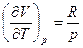
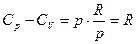
Заметим, что 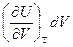 - работа, которую совершает система, преодолевая внутренние силы сцепления. Производная
- работа, которую совершает система, преодолевая внутренние силы сцепления. Производная 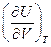 имеет размерность давления и называется внутренним давлением.
имеет размерность давления и называется внутренним давлением.
2.6. Уравнение адиабаты идеального газа.
dQ = dU + pdV
Для идеального газа dU = CVdT, следовательно
dQ = CvdT + pdV и если процесс адиабатический dQ = 0
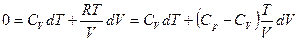
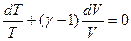 где
где 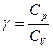
CV и Cp для идеального газа не зависят от температуры
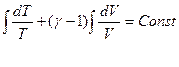
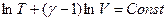
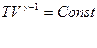
Поскольку 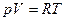 , то
, то 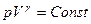 (Уравнение Пуассона)
(Уравнение Пуассона)
| γ | одноатомного газа | 5/3 | 1,67 |
| γ | двухатомного газа | 7/5 | 1,4 |
| γ | трех и многоатомного | 8/6 | 1,33 |
Для газов величину γ можно определить, измеряя скорость звука в газе :
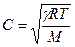 - скорость звука в газе, имеющим мольную массу М
- скорость звука в газе, имеющим мольную массу М
Дата добавления: 2015-07-30; просмотров: 912;
