Полный дифференциал внутренней энергии открытой системы можем записать

как

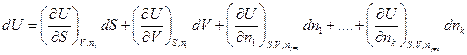
Индекс n_j≠i означает, что число молей других веществ, кроме данного, не изменяется.

Но если открытая система изменяет свое состояние при постоянном составе (все n_i =const), то она ничем не отличается от закрытой системы, поэтому

и

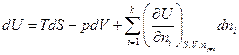
Гиббс назвал частную производную 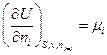химическим

потенциалом i –ого компонента.

Аналогично

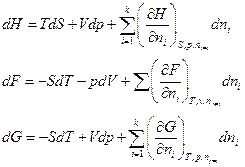
Поскольку H≡ U + pV, F ≡ U – TS, G ≡ U – TS + pv

то dH = dU + pdV + Vdp

dF = dU – TdS – SdT

dG = dU – TdS – SdT + Vdp + pdV

и подставив сюда

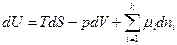
получаем

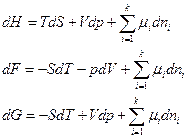
Сравнив выражение для полных дифференциалов характеристических функций, получаем

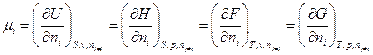
т.е. химический потенциал компонента равен приращению характеристической функции системы при добавлении одного моля данного компонента при условии, что естественные переменные и состав системы остаются постоянными, т.е. система достаточно велика.

7.3. Однородные функции. Уравнение Гиббса-Дюгема.

Функция многих переменных, например F(x,y,z), называется однородной функцией порядка k, если она обладает следующим свойством:

F ( tx, ty, tz ) = t^k F ( x, y, z )

( например, F = x³ +x²y + y²x + z³ является однородной функцией 3-его порядка). Однородные функции обладают следующим свойством (теорема Эйлера) :

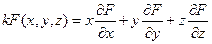
Доказательство теоремы Эйлера следующее.

Если f = f (x₁, x₂,…x_n ), а каждое x_i = φ( t ) то

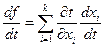
Пусть F ( x, y, z ) - однородная функция порядка k, положим x = tα, y=tβ, z = tγ,

тогда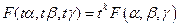

Продифференцируем по t :

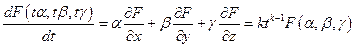
Положим t = 1, тогда α = x, β = y γ = z и

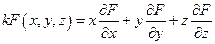
что и требовалось доказать.

Если температура и давление постоянны, то энергия Гиббса является функцией только числа молей компонентов:

G = G (n₁, n₂, …n_k )

и легко сообразить, что она является однородной функцией первого порядка относительно числа молей компонентов и по теореме Эйлера (k = 1)

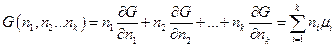
После дифференцирования имеем:

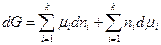
Но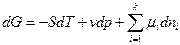

а при p, T =const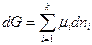

Следовательно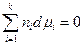

Это уравнение называется уравнением Гиббса-Дюгема и широко применяется в термодинамике растворов поскольку дает возможность рассчитать dμ_i i –ого компонента, если известны изменения химических потенциалов всех остальных компанентов в изобарно-изотермическом процессе. Для бинарного раствора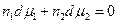

Разделив на сумму п₁ +п₂ получим

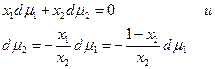
7.4. Условия равновесия в многокомпонентных гетерогенных системах.

Пусть р,Т = Const , тогда

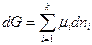
Если в системе имеются фазы ( ' ) и ( '' ), то при переходе dn_i молей i –ого компонента из фазы ( ' ) в фазу ( '' ) изменение энергии Гиббса системы dG будет складываться из изменении энергий Гиббса обеих фаз dG 'и dG ''

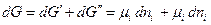
Если система закрытая, то

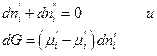
а если она к тому же и равновесна, то dG = 0 и, следовательно,

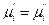
т.е. химические потенциалы данного компонента во всех фазах системы, находящейся в равновесии, равны между собой.

Самопроизвольный неравновесный процесс может идти только в сторону уменьшения энергии Гиббса системы dG < 0 ( p,T = const ).

Предположим, что 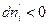, т.е. фаза ( ' ) теряет i –ый компонент, но

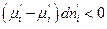значит .

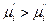Если же 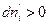, тогда 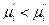. Таким образом, компонент самопроизвольно переходит из фазы, в которой его химический потенциал больше, в фазу, в которой его химический потенциал меньше.

Эти условия равновесия и самопроизвольности процессов переноса вещества в многокомпонентных системах являются обобщением таковых для однокомпонентных систем (см. гл. 6 ). Кроме того легко заметить, что химический потенциал чистого вещества равен его мольной энергии Гиббса.