В этом случае выражение (61) имеет вид
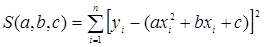 .
.
Это функция трех переменных a, b, с. Система уравнений (62) принимает вид
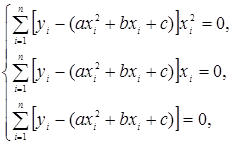
или в развернутом виде:
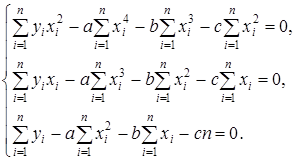
Получаем систему линейных уравнений для определения неизвестных а, b, с. Из характера задачи следует, что система имеет определенное решение и что при полученных значениях а, b, с функция S(а, b, с) имеет минимум.
Пример 44.Пусть на основании эксперимента получены четыре значения искомой функции у = j(х) при четырех значениях аргумента (п = 4), которые записаны в таблице:
| х | ||||
| у | 2,5 | 0,5 |
Будем искать функцию j в виде линейной функции у = ах + b. Составляем выражение S(a, b):
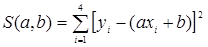 .
.
Для составления системы (63) для определения коэффициентов а и b предварительно вычисляем
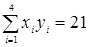 ,
, 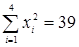 ,
, 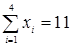 ,
, 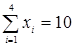 .
.
Система (63) принимает вид
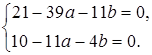
Решая эту систему, находим а и b: а = -26/35, b = 159/35. Искомая прямая есть:
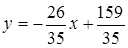 .
.
Задание для самостоятельной работы
146.На основании эксперимента получены значения искомой функции у = j(х) при пяти значениях аргумента (п = 5), которые записаны в таблице:
| х | -1 | ||||
| у | -3 | -0.5 |
Найти функцию j в виде линейной функции у = ах + b.
147.На основании эксперимента получены четыре значения искомой функции у = j(х) при четырех значениях аргумента (п = 4), которые записаны в таблице:
| х | ||||
| у |
Найти функцию j в виде функции y = ax2 + bx + c.
Дата добавления: 2015-07-24; просмотров: 1179;
