Особые точки кривой
Понятие частной производной используется при исследовании кривых.
Пусть кривая задана уравнением
F(х, у) = 0.
Угловой коэффициент касательной к кривой определяется по формуле
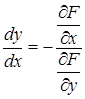 .
.
Если в данной точке М(х, у) рассматриваемой кривой по крайней мере одна из частных производных 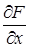 и
и 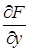 не обращается в нуль, то в этой точке вполне определяется или
не обращается в нуль, то в этой точке вполне определяется или 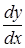 или
или 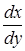 . Кривая F(х, у) = 0 в такой точке имеет вполне определенную касательную. В этом случае точка М(х, у) называется обыкновенной точкой.
. Кривая F(х, у) = 0 в такой точке имеет вполне определенную касательную. В этом случае точка М(х, у) называется обыкновенной точкой.
Если же в некоторой точке М0(х0, у0) имеем
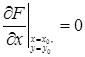 или
или 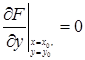 ,
,
то угловой коэффициент касательной становится неопределенным.
Определение. Если в точке М0(х0, у0) кривой F(х, у) = 0 обе частные производные 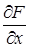 и
и 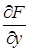 обращаются в нуль, то такая точка называется особой точкой кривой. Следовательно, особая точка кривой определяется системой уравнений
обращаются в нуль, то такая точка называется особой точкой кривой. Следовательно, особая точка кривой определяется системой уравнений
F = 0, 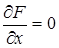 ,
, 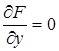 .
.
Естественно, что не всякая кривая имеет особые точки. Так, например, для эллипса
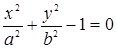 ,
,
очевидно,
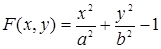 ,
, 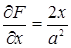 ,
, 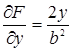 ,
,
производные 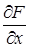 и
и 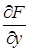 обращаются в нуль только при х = 0, у = 0, но эти значения х и у не удовлетворяют уравнению эллипса. Следовательно, эллипс не имеет особых точек.
обращаются в нуль только при х = 0, у = 0, но эти значения х и у не удовлетворяют уравнению эллипса. Следовательно, эллипс не имеет особых точек.
Не предпринимая подробного исследования поведения кривой вблизи особой точки, рассмотрим несколько примеров кривых, имеющих особые точки.
Пример 45. Исследовать особые точки кривой
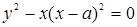 , (а > 0).
, (а > 0).
Решение. В данном случае 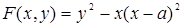 , поэтому
, поэтому
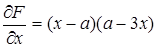 ,
, 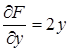 .
.
Решая совместно три уравнения
F = 0, 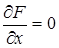 ,
, 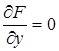 ,
,
находим единственную удовлетворяющую им систему значений х и у:
х0 = а, у0 = 0.
Следовательно, точка М0(а, 0) есть особая точка кривой.
Исследуем поведение кривой вблизи особой точки и построим кривую. Перепишем данное уравнение в виде 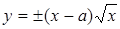 . Из этой формулы следует, что кривая: 1) определена лишь при х ³ 0; 2) симметрична относительно оси Ох; 3) пересекает ось Ох в точках (0, 0) и (а, 0). Последняя точка, как было указано, является особой.
. Из этой формулы следует, что кривая: 1) определена лишь при х ³ 0; 2) симметрична относительно оси Ох; 3) пересекает ось Ох в точках (0, 0) и (а, 0). Последняя точка, как было указано, является особой.
Мы рассмотрим сначала ту часть кривой, которая соответствует знаку +:  . Найдем первую и вторую производные от у по х:
. Найдем первую и вторую производные от у по х:
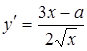 ,
, 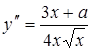 .
.
При х = 0 имеем 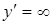 . Следовательно, кривая касается оси Оу в начале координат. При х = а/3 имеем
. Следовательно, кривая касается оси Оу в начале координат. При х = а/3 имеем 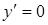 ,
, 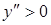 , т.е. при х = а/3 функция у имеет минимум:
, т.е. при х = а/3 функция у имеет минимум: 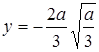 . На отрезке 0 < х < а имеем у < 0; при х > а/3 будет
. На отрезке 0 < х < а имеем у < 0; при х > а/3 будет 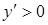 ; при х ® ¥ будет у ® ¥. При х = а имеем
; при х ® ¥ будет у ® ¥. При х = а имеем 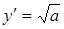 , т.е. в особой точке М0(а, 0) ветвь кривой
, т.е. в особой точке М0(а, 0) ветвь кривой  имеет касательную
имеет касательную 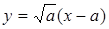 .
.
Так как вторая ветвь кривой 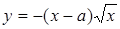 симметрична с первой относительно оси Ох, то, следовательно, в особой точке кривая имеет и вторую касательную (ко второй ветви)
симметрична с первой относительно оси Ох, то, следовательно, в особой точке кривая имеет и вторую касательную (ко второй ветви) 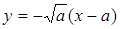 .
.
Через особую точку кривая проходит дважды. Такая точка называется узловой точкой.
Рассмотренная кривая изображена на рис. 10.
 |  |
Пример 46. Исследовать на особые точки кривую (полукубическая парабола) у2 – х3 = 0.
Решение. Координаты особых точек определяются из системы уравнений: у2 – х3 = 0, 3х2 = 0, 2у = 0. Следовательно, М0(0, 0) есть особая точка.
Перепишем данное уравнение в виде  . Для построения кривой исследуем сначала ветвь, которой в уравнении соответствует знак плюс; ветвь кривой, соответствующая знаку минус, симметрична с первой относительно оси Ох.
. Для построения кривой исследуем сначала ветвь, которой в уравнении соответствует знак плюс; ветвь кривой, соответствующая знаку минус, симметрична с первой относительно оси Ох.
Функция у определена только при х ³ 0, неотрицательна и возрастает при возрастании х.
Найдем первую и вторую производные от функции 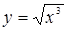 :
:
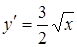 ,
, 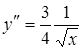 .
.
При х = 0 имеем у = 0, у¢ = 0. Следовательно, рассматриваемая ветвь кривой имеет в начале координат касательную у = 0. Вторая ветвь кривой 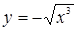 также проходит через начало координат и имеет ту же касательную у = 0. Таким образом, две различные ветви кривой встречаются в начале координат, имеют одну и ту же касательную и расположены от касательной по разные стороны. Такая особая точка называется точкой возврата первого рода (рис. 11).
также проходит через начало координат и имеет ту же касательную у = 0. Таким образом, две различные ветви кривой встречаются в начале координат, имеют одну и ту же касательную и расположены от касательной по разные стороны. Такая особая точка называется точкой возврата первого рода (рис. 11).
Заметим, что кривую у2 – х3 = 0 можно рассматривать как предельный случай кривой у2 = х(х – а)2 (рассмотренной в примере 45), когда а ® 0, т.е. когда петля кривой стягивается в точку.
Пример 47. Исследовать кривую (у – х2)2 – х5 = 0.
Решение. Координаты особых точек определяются системой уравнений
- 4х(у – х2) – 5х4 = 0, 2(у – х2) = 0,
которая имеет единственное решение: х = 0, у = 0. Следовательно, начало координат есть особая точка.
Перепишем данное уравнение в виде 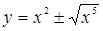 . Из этого уравнения следует, что х может принимать значения от 0 до +¥.
. Из этого уравнения следует, что х может принимать значения от 0 до +¥.
Определим производные первого и второго порядка:
 ,
, 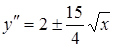 .
.
Исследуем ветви кривой, соответствующие знакам плюс и минус, в отдельности. В обоих случаях при х = 0 имеем: у = 0, у¢ = 0, т.е. для обеих ветвей оси Ох является касательной. Рассмотрим сначала ветвь 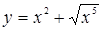 . При возрастании х от 0 до ¥, у возрастает от 0 до ¥. Вторая ветвь
. При возрастании х от 0 до ¥, у возрастает от 0 до ¥. Вторая ветвь 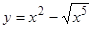 пересекает ось Ох в точках (0, 0) и (1, 0).
пересекает ось Ох в точках (0, 0) и (1, 0).
При х = 16/25 функция 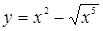 имеет максимум. Если х ® +¥, то у ® -¥.
имеет максимум. Если х ® +¥, то у ® -¥.
|
 |  |
|





Таким образом, в данном случае в начале координат встречаются две ветви кривой; обе ветви имеют одну и ту же касательную и расположены по одну сторону от касательной вблизи точки касания. Такая особая точка называется точкой возврата второго рода. График рассматриваемой функции изображен на рис. 12.
Пример 48. Исследовать кривую у2 – х4 + х6 = 0.
Решение. Начало координат есть особая точка. Для исследования кривой вблизи этой точки перепишем уравнение кривой в виде  .
.
Так как уравнение кривой содержит только четные степени переменных, то кривая симметрична относительно осей координат и, следовательно, достаточно исследовать часть кривой, соответствующую положительным значениям х и у. Из последнего уравнения следует, что х может изменяться на отрезке от 0 до 1, т.е. 0 £ х £ 1.
Вычислим первую производную для той ветви кривой, которая является графиком функции  :
:
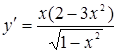 .
.
При х = 0 имеем у = 0, у¢ = 0. Следовательно, в начале координат кривая касается оси Ох.
При х = 1 имеем у = 0, у¢ = ¥; следовательно, в точке (1, 0) касательная параллельна оси Оу. При  функция имеет максимум (рис. 13).
функция имеет максимум (рис. 13).
В начале координат (в особой точке) две ветви кривой, соответствующие знакам плюс и минус перед корнем, взаимно касаются. Такая особая точка называется точкой соприкосновения.
Пример 49. Исследовать кривую у2 – х2(х – 1) = 0.
Решение. Напишем систему уравнений, определяющих особые точки:
у2 – х2(х – 1) = 0, -3х2 + 2х = 0, 2у = 0.
Эта система имеет решение х = 0, у = 0. Следовательно, точка (0, 0) есть особая точка кривой. Перепишем данное уравнение в виде  . Очевидно, что х может изменяться от 1 до +¥, а также принимать значение 0 (в последнем случае у = 0).
. Очевидно, что х может изменяться от 1 до +¥, а также принимать значение 0 (в последнем случае у = 0).
Исследуем ветвь кривой, соответствующую знаку плюс перед корнем. При увеличении х от 1 до ¥ у увеличивается от 0 до ¥. Производная 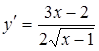 . При х = 1 имеем у¢ = ¥; следовательно, в точке (1, 0) касательная параллельна оси Оу.
. При х = 1 имеем у¢ = ¥; следовательно, в точке (1, 0) касательная параллельна оси Оу.
Вторая ветвь кривой, соответствующая знаку минус, симметрична с первой относительно оси Ох.
Точка (0, 0) имеет координаты, удовлетворяющие уравнению, и, следовательно, принадлежит кривой, но вблизи нее нет других точек кривой (рис. 14). Такая особая точка называется изолированной особой точкой.

Задание для самостоятельной работы
Исследовать на особые точки кривые:
148.  . .
| 150. 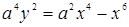 . .
|
149. 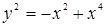 . .
| 151.  . .
|
152. 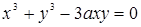 (декартов лист). (декартов лист).
| 153. 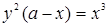 (циссоида). (циссоида).
|
154. 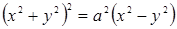 (лемниската). (лемниската).
| 155.  (строфоида). (строфоида).
|
156. 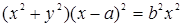 (a > 0, b > 0) (конхоида). Рассмотреть три случая:
(a > 0, b > 0) (конхоида). Рассмотреть три случая:
1) a > b, 2) a = b, 3) a < b.
157. Выяснить изменение характера особой точки кривой
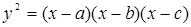
в зависимости от значений a, b, c (a  b
b  c вещественны).
c вещественны).
Дата добавления: 2015-07-24; просмотров: 3202;
