Основное уравнение МКТ
Молекулярно-кинетический и термодинамический методы изучения макроскопических систем. Статистическая физика.
Молекулярная физика и термодинамика - разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: молекулярно-кинетический (статистический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики.
Молекулярная физика – это раздел физики, изучающий физические свойства тел в различных агрегатных состояниях, исходя из так называемых молекулярно-кинетических представлений. В основе МКТ лежат следующие положения:
1. Все тела состоят из большого количества микроскопических обособленных частиц.
2. Молекулы вещества находятся в непрерывном хаотичном (тепловом) движении.
3. Свойства макроскопических тел объясняются взаимодействием молекул, из которых они состоят.
Взаимодействие существенно зависит от типа молекул и расстояний между ними. В частности, зависимостью молекулярных сил от межмолекулярных расстояний объясняется качественное различие тел, находящихся в разных агрегатных состояниях (твердом, жидком, газообразном).
Процессы, изучаемые молекулярной физикой, являются результатом действия огромного числа молекул. Свойства большого числа молекул отличны от свойств каждой отдельной молекулы и подчиняются статистическим закономерностям. Они изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью беспорядочного движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.
Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений» Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных.
Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества.
Таким образом, для изучения макроскопических процессов в телах применяют два метода исследования: молекулярно-кинетический (статистический) и термодинамический. Эти методы, необходимо рассматривать как единое целое, они взаимно дополняют друг друга и находят широкое практическое применение в современной физике.
Основное уравнение МКТ связывает параметры состояния газа с характеристиками движения его молекул, т. е. устанавливает зависимость между давлением и объемом газа и кинетической энергией поступательного движения его молекул.
Для вывода уравнения рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку ΔS (рис. 1) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула массой то, движущаяся перпендикулярно площадке, передает стенке сосуда импульс
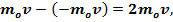
где v — скорость молекул газа.
За время Δt площадки ΔS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием ΔS и высотой vΔt (рис.1). Число этих молекул равно nΔSvΔt (п— концентрация молекул).
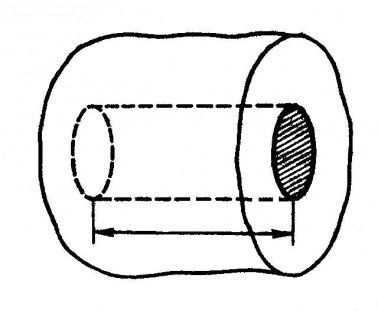
| vΔt |
| ΔS |
Рис. 1.
Необходимо, однако, учитывать, что реально молекулы движутся к площадке ΔS под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул (1/6) движется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку ΔS будет 1/6 nΔSvΔt. При столкновении с площадкой эти молекулы передадут ей импульс
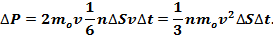
Тогда давление газа, оказываемое им на стенку сосуда,
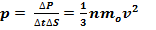 (6)
(6)
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2, …,vN, то целесообразно рассматривать среднюю квадратичную скорость,характеризующую всю совокупность молекул газа.
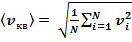 (7)
(7)
Уравнение (6) с учетом (7) примет вид
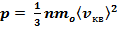 (8)
(8)
Выражение (8) называется основным уравнением молекулярно-кинетической теории идеальных газов.
Учитывая, что п = N / V, получим
 (9)
(9)
или
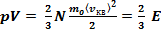 (10)
(10)
где E — суммарная кинетическая энергия поступательного движения всех молекул газа.
Так как масса газа т = Nmo, то уравнение (9) можно переписать в виде
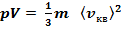
Для одного моля газа т = M(M — молярная масса), поэтому
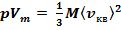 ,
,
где Vm — молярный объем.
С другой стороны, по уравнению Клапейрона — Менделеева, рV = RT. Таким образом,
RT 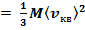
откуда
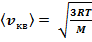 (11)
(11)
Так как M =moNA, где т — масса одной молекулы, a NA — постоянная Авогадро, то из уравнения (11) следует, что
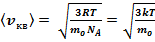 (12)
(12)
где k = R/N — постоянная Больцмана.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа пропорциональна термодинамической температуре и зависит только от нее.
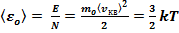 (13)
(13)
Из этого уравнения следует, что при Т = 0,  = 0, т.е. при ОКпрекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа и формула (13) раскрывает молекулярно-кинетическое толкование температуры.
= 0, т.е. при ОКпрекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа и формула (13) раскрывает молекулярно-кинетическое толкование температуры.
Дата добавления: 2015-08-11; просмотров: 1305;
