Позиционные задачи. 2–я ГПЗ – пересечение двух поверхностей.

2–я ГПЗ – пересечение двух поверхностей.

Результатом пересечения двух поверхностей будет линия (или линии), точки которых одновременно принадлежат обеим поверхностям.

Пример 1. Пересечение двух плоскостей общего положения Г и S (Рис.47).

Две плоскости пересекаются по прямой линии. Поэтому для ее построения достаточно определить две точки искомой линии пересечения

Г (АВС)хS (сIId)= e.

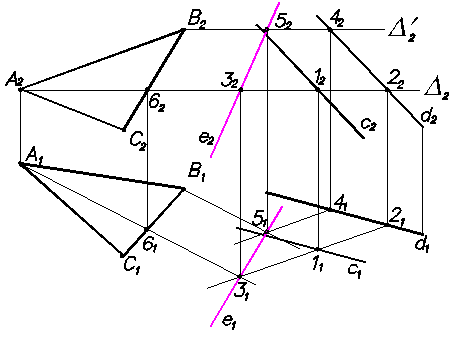Рис.47

Проводим фронтально-проецирующую плоскость D(D2) и определяем прямые, по которым дополнительная плоскость D пересечет заданные плоскости ГиS.

DхГ = А6; DхS = 12;

На приведенном Рис.47 мы видим, что прямые А6 и 12, находясь в одной плоскости D, пересекаются в точке 3, принадлежащей искомой прямой e.

Для нахождения точки 5 линии пересечения e, проведем вторую фронтально-проецирующую плоскость D' (D'2). Для упрощения построений плоскость D'(D'2)проведем через точку В (В2) и D'II D.Дальнейшие построения видны из Рис.88.

Полученные точки 3 и 5 однозначно определяют искомую прямую e ( e = ГxS ).

В общем случае линией пересечения двух поверхностей является пространственная линия. Строят такие линии последовательно, по точкам, используя для этой цели поверхности – посредники. В большинстве случаев в качестве посредников используют либо плоскости, либо сферы, которые пересекают исходные поверхности по удобным для построения линиям – прямым или окружностям.

Способы вспомогательных плоскостей, в свою очередь, разделяются на способы вспомогательных проецирующих плоскостей и вспомогательных плоскостей общего положения.

Существует также два варианта использования в качестве посредника сферических поверхностей:

- семейство концентрических сфер переменного радиуса;

- семейство эксцентрических сфер постоянного или переменного

радиуса.

Применение любого из вышеуказанных способов обусловлено

типом пересекающихся поверхностей, их взаимным расположением, а также их ориентацией относительно плоскостей проекций.

Пример 2 Построение линии пересечения двух поверхностей вращения (Рис.48).

DхГ = n = ?

Рис.48

Так как у данных пересекающихся поверхностей имеется общая плоскость симметрии и эта плоскость параллельна фронтальной плоскости проекций, построение линии пересечения следует начинать с построения проекций точек, принадлежность которых будущей линия пересечения n очевидна. В нашем случае это точки 1 и 2 (результат пересечения лежащих в одной плоскости контурных образующих обеих поверхностей.

Для решения данной задачи в качестве посредника будет использовано семейство фронтально-проецирующих плоскостей уровня S', S' ', S' ' ' ( S', S' ', S' ' ' ^ П2иS', S' ', S' ' 'IIП1).

Такой выбор обусловлен тем, что плоскости – посредники пересекут заданные поверхности Dи Г по окружностям, которые на горизонтальную плоскость проекций спроецируются без искажений.

Дальнейшее решение задачи аналогично решению, приведенному в примере 1 (Рис.47).