Способ вспомогательных плоскостей общего положения.
При решении задач по определению точек пересечении линейчатых поверхностей (конических, цилиндрических, пирамидальных и призматических) с прямыми общего положения в качестве плоскостей – посредников используют плоскости общего положения. Такая плоскость, к примеру, проведенная через вершину конической поверхности и заданную прямую общего положения, пересекает коническую поверхность по двум образующим. Точки пересечения полученных образующих с исходной прямой общего положения (рассматриваемые прямые принадлежат одной плоскости) и являются точками пересечения заданных в условии задачи прямой общего положения и конической поверхности.
Пример. Построить точки пересечения прямой общего положения а и конической поверхности вращения D (Рис.49).
1-я ГПЗ;Алгоритм 3.
а х D = А,В =?
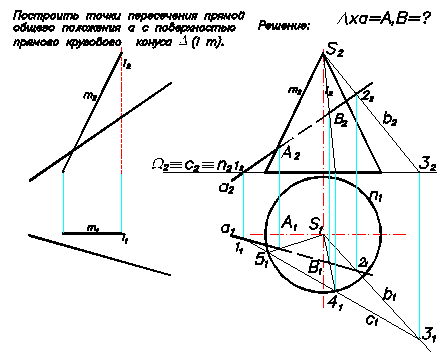
Рис.49
Для решения данной задачи используем в качестве посредника плоскость общего положения Г( S; a).Также необходимо ввести фронтально проецирующую плоскость уровня W (W2).Плоскость Wсовпадает с плоскостью основания конической поверхности ( W2 = n2).
Построим линию пересечения c двух вспомогательных плоскостей ( Г и W ).
Г х W = c = ?
Для этого в плоскости Г проведем дополнительную прямую b.
Прямые а и b , принадлежащие плоскости Г, пересекут плоскость W
в точках 1 и 3 соответственно, которые и определят прямую c(1,3), по которой пересекаются плоскости Г и W .
a Ì Г; ахW = 1; b Ì Г; bxW = 3;
Точки1и3определяют прямуюс.
Окружность n основания конической поверхности D и прямая cпринадлежат плоскости W,и поэтомупересекаются в точках 4 и 5. Прямые S4 и S5 принадлежат плоскости Г, так как
точка SÌ Г; точка 4 Ì с и точка 5 Ì с, асÌ Г.
Одновременно заключаем, что прямые S4 и S5 являются образующими конической поверхности D, так как точка S является вершиной конической поверхности D,а точки 4 и 5 принадлежат окружности n основания этой поверхности. На основании вышеизложенного делаем вывод, что плоскость общего положения Г пересекает коническую поверхность по образующим S4 и S5.
Но прямая а принадлежит плоскости Г по определению плоскости Г. Из чертежа видно, что горизонтальная проекция а1 прямой а пересекается с горизонтальными проекциями S141 и S151 прямолинейных образующих S4 и S5 конической поверхности D. Из вышесказанного мы знаем, что прямые а, S4 и S5 принадлежат одной плоскости Г.
Из этого мы делаем вывод, что точки А и В( А = а х S4; B = ax S5) являются точками пересечения прямой ас конической поверхностью D.
Часть прямой а между точками А и В на обеих проекциях будет невидимой как находящаяся «внутри» конической поверхности D. Определение видимости остальных частей проекций а1 и а2 прямой а, как не представляющее особой сложности, предлагается выполнить самостоятельно.
Дата добавления: 2015-08-11; просмотров: 1007;
