Позиционные задачи

II. Один из пересекающихся геометрических образов занимает проецирующее положение.

1-я ГПЗ – пересечение линии и поверхности.

Результатом пересечения линии и поверхности будет точка (или точки), которые одновременно принадлежат обоим пересекающимся Г. О. (линии и поверхности).

Пример 1. Пересечение прямой общего положения а с фронтально

проецирующей плоскостью Г (Рис.41):

а х Г = К = ?(Г ^ П2).

Г2- главная (вырожденная) проекция плоскости Г на П2;

Ниже приводится порядок (алгоритм) решения таких задач.

Рис.41

Фронтальная проекция точки пересечения (К2)плоскости Г и прямой а очевидна. Она совпадает с точкой пересечения фронтальных проекций пересекающихся геометрических образов. Горизонтальную проекцию точки К (К1)находим по ее принадлежности образу, не занимающему проецирующее положение, а именно, прямой а. Для этого определяем горизонтальную проекцию точки К, проведя линию связи от точки К2 до ее пересечения с прямой а1 в точке К1.

Пример 2 Пересечение горизонтально проецирующей прямой n с поверхностью сферы (Рис.42).

nхS = А,А' = ? n ^П1;

n1 - главная (вырожденная) проекция прямой п на П1;

Решение задачи аналогично решению, приведенному в примере 1.

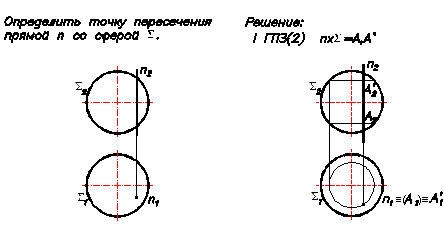
Рис.42

2–я ГПЗ – пересечение двух поверхностей.

Результатом пересечения двух поверхностей будет линия (или линии), точки которых одновременно принадлежат обеим поверхностям.

Пример 1. Пересечение фронтально проецирующей плоскости Г с поверхностью сферы S (Рис.43)

Г х S = а = ?; Г ^ П2.

Г2 - главная (вырожденная) проекция плоскости Г на П2;

Рис.43

Фронтальная проекция линии пересечения а2 совпадает с главной проекцией Г2 плоскости Г. Проекция а2 также ограничена контурной линией (окружностью) фронтальной проекции S2 поверхности S (расположена внутри окружности). Горизонтальную проекцию линии пересечения а1 определяют по ее принадлежности геометрическому образу, не занимающему проецирующего положения (проекции сферы S1). После этого необходимо определить видимость проекций а1 и а2 линии пересечения поверхностей и На фронтальной проекции а2 линии пересечения а видимый и невидимый участки совпадают (принадлежат одной фронтально проецирующей плоскости Г). Фронтально конкурирующие точки 1 и 2 (12=22) являются точками, разделяющими видимость горизонтальной проекции а1 линии пересечения а. На горизонтальной проекции видимой будет та часть проекции а1 линии пересечения а, которая на фронтальной плоскости проекций расположена на верхней половине проекции сферы.

В ряде случаев мы заранее знаем типы кривых, которые получаются при пересечении, к примеру, плоскостями поверхностей вращения. Такие кривые могут быть построены по основным элементам, определяющим эти кривые.

Рассмотрим, какие могут получиться кривые при пересечении плоскостями конуса вращения (ось конуса вращения занимает горизонтально проецирующее положение; коническая поверхность пересекается фронтально проецирующими плоскостями; 2-я ГПЗ, алг.2, Рис.44).

1. Секущая плоскость не параллельна ни одной из образующих конуса [пересекает все образующие; ( I )]. В сечении получается эллипс. Построение эллипса можно свести к определению его центра и двух осей или сопряженных диаметров.

2. Секущая плоскость параллельна контурной образующей ( II). В сечении получается парабола.

3.Секущая плоскость параллельна двум образующим ( III ). В сечении получается гипербола.

4. Секущая плоскость проходит через вершину конуса ( IV). В сечении две прямые.

Рис.44 (образующие конуса).

5. Секущая плоскость перпендикулярна оси конуса вращения (V ). В сечении получается окружность.

6. У плоскости VI с конической поверхностью одна общая точка – вершина конуса.

При решении позиционных задач на пересечение поверхностей наибольшую сложность представляют случаи, когда ни один из пересекающихся геометрических образов не занимает проецирующего положения. Общим способом решения таких задач является использование посредников. Наиболее часто используемыми посредниками являются:

- проецирующие поверхности;

- сферы (концентрические и эксцентрические);

- плоскости общего положения.

1-я ГПЗ – пересечение линии и поверхности.

Результатом пересечения линии и поверхности будет точка (или точки), которые одновременно принадлежат обоим пересекающимся Г. О. (линии и поверхности).

Пример 1. Пересечение прямой а и плоскости общего положения S(АВС) (Рис.45):

а х S= D = ?

Ниже приводится порядок (алгоритм) решения таких задач.

Построить точку пересечения плоскости S (АВС) и прямой а;

S(АВС) – плоскость общего положения; а - прямая общего положения.

Для решения данной задачи в качестве посредника используем фронтально проецирующую плоскость Г, проекция Г2 которой совпадает с фронтальной проекцией прямой а. Г2= а.

Плоскость Г пересечет исходную плоскость S по прямой b, фронтальная проекция которой b2 (12, 22) совпадает с фронтальной проекцией Г2 плоскости Г. Построить горизонтальную проекцию b1(11,21) прямой b не составит труда.

Поскольку обе прямые а и b одновременно принадлежат плоскости Г, то точка их пересечения D (D1 = a1 x 1121; D2Ì a2) и будет точкой пересечения прямой а с плоскостью S.

После этого, используя метод конкурирующих точек, определяем на обеих проекциях видимость прямой а. Проекции точки D (D1 и D2) разделяют проекции прямой а (а1 и а2) на видимый и невидимый участки на плоскостях проекций П1 и П2 соответственно.

Рис.45