Поверхности вращения с образующей - окружностью.

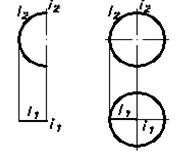Рассмотрим только такие поверхности вращения, у которых ось вращения лежит в плоскости окружности. Ось вращения совпадает с диаметром окружности. Получаемая поверхность – сфера (Рис.33).

Рис.33

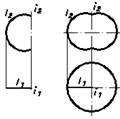
«Несет» на себе три семейства концентрических окружностей переменного радиуса, лежащих в плоскостях, параллельных плоскостям проекций.

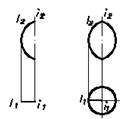
Ось вращения не проходит через центр окружности. Образованные при вращении поверхности называются торами. Торы,приведенные на Рис.34, называются закрытыми.

Рис.34

На закрытых торах имеется одно семейство концентрических окружностей переменного радиуса, лежащих в плоскостях, перпендикулярных осям вращения.

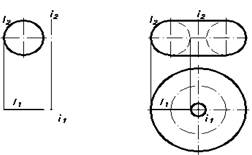Если ось вращения проходит вне окружности, полученная поверхность называется кольцом(открытый тор; Рис.35). При пересечении кольца плоскостями, перпендикулярными его оси i, мы получим два семейства концентрических окружностей переменного радиуса.

Рис.35

Их условно можно назвать семействами внутренних и наружных окружностей кольца. При пересечении кольца плоскостями, проходящими через его ось i, мы получим семейство окружностей постоянного радиуса, равного радиусу образующей окружности. Центры этого семейства окружностей принадлежат окружности а, сформированной при вращении центра О образующей окружности n вокруг оси i (Рис.35). Также окружности этого семейства «лежат» в плоскостях, нормальных (перпендикулярных) окружности а.

Сфера – поверхность второго порядка, а кольцо – четвертого (максимальное число точек возможного пересечения поверхности прямой линией).

1. Эллипсоид вращения образуется вращением эллипса вокруг его осей.

Форма эллипсоида вращения зависит от выбранной оси вращения (одно семейство удобных для построения линий – концентрические окружности переменного радиуса в плоскостях, перпендикулярных оси вращения).

2. Параболоид вращения образуется вращением параболы вокруг оси.

(Отражатель прожектора. При расположении источника света в точке фокуса на выходе мощный параллельный пучок света).

1. Однополостный гиперболоид вращения образуется вращением

гиперболы вокруг мнимой оси. Одно семейство удобных для построения линий - концентрические окружности переменного радиуса в плоскостях, перпендикулярных оси вращения.

2. Двухполостный гиперболоид вращения образуется вращением

гиперболы вокруг действительной оси. Одно семейство удобных для построения линий - концентрические окружности переменного радиуса в плоскостях, перпендикулярных оси вращения.

Четыре последних поверхности являются поверхностями второго порядка.

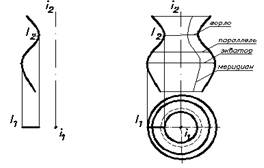
Поверхность вращения общего вида (Рис.36)

Образуется при вращении любой линии, как плоской, так и

пространственной, вокруг неподвижной оси. Каждая точка образующей при вращении описывает окружность, лежащую в плоскости, перпендикулярной оси вращения и с центром, лежащим на оси вращения.

Рис.36

Полученные окружности называются параллелями поверхности вращения.

Минимальная окружность – горло поверхности вращения.

Максимальная окружность – экватор поверхности вращения.

Линии поверхности вращения, лежащие в плоскостях, проходящих через ось вращения, называются меридианами.Естественно, что все меридианы одинаковы по форме и по своим размерам. Меридиан, лежащий в плоскости, параллельной плоскости проекции, называется главным меридианом. Он формирует очерк поверхности.

Поверхность вращения общего вида также несет на себе одно семейство удобных для построения линий - концентрические окружности переменного радиуса, лежащие в перпендикулярной оси вращения плоскости проекций.

Лекция 6.

Позиционные задачи: