Решение главных позиционных задач

I. Оба пересекающихся геометрических образа занимают

проецирующее положение (1-й алгоритм решения):

1-я ГПЗ – пересечение линии и поверхности.

Результатом пересечения линии и поверхности будет точка (или точки), которые одновременно принадлежат обоим пересекающимся Г. О. (линии и поверхности).

Пример 1. Пересечение фронтально проецирующей прямой n и горизонтально проецирующей плоскости S (Рис.37):

nхS = А = ? n ^ II1 и S ^П2;

n2 - главная (вырожденная) проекция прямой п на П2;

S1- главная (вырожденная) проекция плоскости S на П1;

Ниже приводится порядок (алгоритм) решения таких задач.

1. На П1 и П2 выделяем общие зоны существования проекций пересекающихся Г.О. (точка).

2. Обозначаем точку А (результат пересечения) в пределах выделенных зон.

А2= n2и А1= n1х S1.

Рис.37

Проекции точки пересечения (А1, А2) на плоскостях проекций П1 и П2

совпадают с главными проекциями геометрических образов, занимающих проецирующее положение по отношению к соответствующим плоскостям проекций.

Пример 2 Пересечение фронтально проецирующей прямой n с поверхностью горизонтально проецирующего кругового цилиндра S(Рис.38).

nхS = А,А' = ? n ^ II2 и S ^П1;

n2 - главная (вырожденная) проекция прямой п на П2;

S1- главная (вырожденная) проекция кругового цилиндра S на П1;

Решение задачи аналогично решению, приведенному в примере 1.

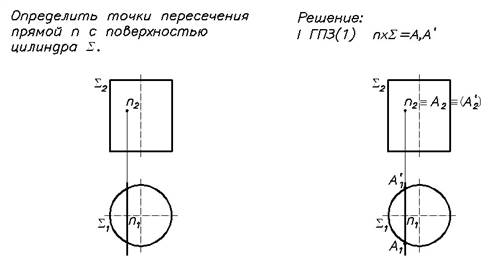Рис.38

2–я ГПЗ – пересечение двух поверхностей.

Результатом пересечения двух поверхностей будет линия (или линии), точки которых одновременно принадлежат обеим поверхностям.

Пример 1. Пересечение фронтально проецирующей плоскости D с поверхностью горизонтально проецирующего кругового цилиндра S (Рис.39)

D х S = m = ?; D ^ П2; S^П1.

D2 - главная (вырожденная) проекция плоскости D на П2;

S1- главная (вырожденная) проекция кругового цилиндра S на П1;

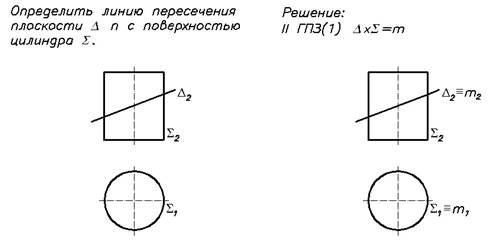
Рис.39

На обеих плоскостях проекций определяем общие зоны существования проекций пересекающихся геометрических образов, в которых и расположены проекции линий пересечения поверхностей D и S.

На П1 проекция линии пересечения (m1) совпадает с главной проекцией поверхности S (m1 = S1);

На П2 проекция линии пересечения представляет собой фрагмент проекции Dограниченный контурными образующими поверхности S.

Пример 2 Пересечение поверхности фронтально проецирующего кругового цилиндра D с поверхностью горизонтально проецирующего кругового цилиндра S(Рис.40).

DхS = n = ? D ^ II2 и S ^П1;

D2 - главная (вырожденная) проекция кругового цилиндра D на П2;

S1- главная (вырожденная) проекция кругового цилиндра S на П1;

Решение задачи аналогично решению, приведенному в примере 1 (Рис.).

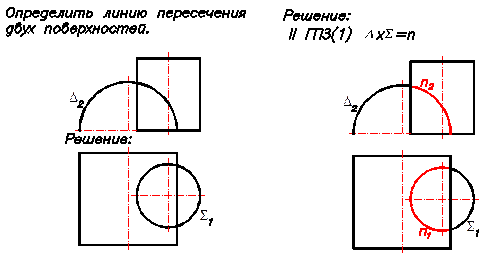
Рис.40