Относительно неподвижной оси
В предыдущем разделе рассмотрено вращательное движение материальной точки. Многие понятия этого раздела легко обобщаются на случай вращательного движения твердого тела конечного размера. Вращательным движением твердого тела называют движение, при котором все точки тела описывают окружности в плоскостях, перпендикулярных оси вращения, при этом их центры лежат на оси вращения. Для кинематического описания вращательного движения достаточно определить в пространстве положение оси вращения, величину угловой скорости, углового ускорения и использовать уравнения кинематики вращательного движения.
Рассмотрим систему, состоящую из n материальных точек. На объекты системы могут действовать внутренние силы, т. е. силы, определяемые взаимодействиями объектов между собой, и внешние силы – силы со стороны тел, не входящих в систему. Для i-й материальной точки механической системы (тела) можно записать уравнение вида (2.40):
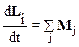 , (j=1, 2, …, n).
, (j=1, 2, …, n).
Запишем аналогичные уравнения для всех элементов системы и сложим их почленно:
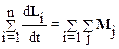 .
. 
Преобразуем левую часть полученного уравнения:
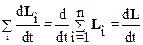 ,
,
где dL/dt=SdLi/dt – момент импульса системы. Отметим, что соотношение (2.43) указывает на аддитивность момента импульса.
Используя третий закон Ньютона и аддитивность момента сил, легко показать, что суммарный момент внутренних сил равен нулю. Таким образом, двойная сумма в правой части уравнения (2.42) равна результирующему моменту внешних сил:
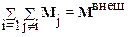 .
.
С учетом сказанного уравнение (2.42) принимает вид:
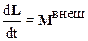 .
.
Это уравнение отличается от уравнения (2.29), записанного для одной материальной точки тем, что теперь L– это момент импульса системы материальных точек относительно точки. Однако, как и для отдельной точки,
· скорость изменения момента импульса механической системы равна моменту внешних сил, действующих на нее.
Если рассматривать вращение системы относительно оси Z, то уравнение (2.45) преобразуется следующим образом:
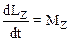 ,
,
где LZ момент импульса системы относительно оси вращения Z, MZ – суммарный момент внешних сил относительно той же оси.
Твердое тело, вращающееся вокруг неподвижной оси с постоянным угловым ускорением (ez = const), можно рассматривать как механическую систему, образованную совокупностью бесконечно малых материальных точек dm. Таким образом, результаты, полученные выше для механической системы, можно использовать при описании движения твердого тела. В частности, применимо уравнение(2.37) в векторнойили скалярной форме:
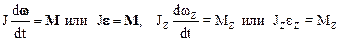
Дата добавления: 2015-08-08; просмотров: 658;
