Момент инерции твердого тела
Момент инерциитвердого тела – величина аддитивная. Момент инерции твердого тела относительно некоторой оси равен арифметической сумме моментов инерции частиц, составляющих это тело, относительно той же оси:
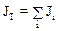 ,
,
здесь Ji – момент инерции i-ой частицы, на которые можно мысленно разбить тело. Говоря иначе, момент инерциитвердого тела относительно некоторой оси равен сумме произведений элементарных масс dmi тела на квадраты расстояний этих масс от той же оси вращения:
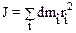 .
.
Для твердого тела, с непрерывным распределением вещества, момент инерции находят интегрированием по объему V, занятым телом:
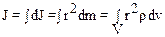 ,
,
где dm=rdV, r – плотность тела, dV – элементарный объем.
B качестве примера вычислим момент инерции однородного диска относительно оси симметрии, перпендикулярной плоскости диска (см. рис. 2.17). Пусть толщина диска h, радиус R, плотность r. Для вычислений воспользуемся полярной системой координат r,j. Элементарная масса частицы диска равна dm=rhrdrdj, элементарный момент инерции dJ==rhr3drdj. Используя (2.49) запишем:
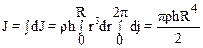 .
.
Произведение prhR2 равно массе М диска, окончательно
 .
.

| Рис. 2.17. К вычислению момента инерции диска. |
Момент инерции однородного тела вращения с некоторой образующей, заданной функцией f(z), вычисляется следующим образом. Пусть твердое тело имеет плотность r. Тогда (см. (2.49))
 ,
,
где L – длина тела вращения.
Таблица 2
Моменты инерции некоторых тел правильной геометрической формы
| Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
| Однородный тонкий стержень массой m и длиной L | Проходит через центр тяжести стержня перпендикулярно стержню | mL2/12 |
| Проходит через конец стержня перпендикулярно стержню | mL2/3 | |
| Тонкое кольцо, обруч, труба радиусом R и массой m, маховик радиусом R и массой m, распределенной по ободу | Проходит через центр перпендикулярно плоскости основания | mR2 |
| Круглый однородный диск (цилиндр) радиусом R и массой m | Проходит через центр диска перпендикулярно плоскости основания | mR2/2 |
| Однородный шар массой m и радиусом R | Проходит через центр шара | 2mR2/5 |
ТеоремуШтейнера примем без доказательства:
· момент инерции тела J относительно оси, не проходящей через его центр масс, равен сумме двух слагаемых. Первое слагаемое равно моменту инерции тела J0 относительно оси, проходящей через центр масс и параллельной данной. Второе слагаемое – произведение массы тела на квадрат расстояния b между осями:
J = J0+mb2.
Дата добавления: 2015-08-08; просмотров: 1211;
