Импульс механической системы

Определение механической системы, как совокупности тел, рассматриваемых в данной задаче, позволяет считать механической системой совокупность материальных точек, материальное тело, а также совокупность материальных тел.

· ИмпульсРмеханической системы, состоящей из N материальных точек (тел) равен векторной сумме импульсов этих точек (тел), входящих в эту систему:

.

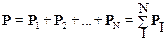Таким образом, импульс – есть величина аддитивная.

При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по величине и направлению скорости и ускорения. Импульс Р тела, имеющего конечные размеры и массу m, движущегося поступательно со скоростью V, равен импульсу материальной точки такой же массы m, движущейся с той же скоростью:

Р=mV.

Заметим, что силы, действующие на материальную точку, всегда происходят от иных материальных точек (тел). На тела механической системы могут действовать силы со стороны тел системы, так и со стороны тел, не входящих в эту систему. Силы взаимодействия между телами системы называются внутренними; силы, действующие со стороны иных тел, называются внешними.

· Внутренние силы– это силы взаимодействия между телами механической системы.

В дальнейшем силы будут обозначаться следующим образом: f_ij – внутренняя сила, действующая на i-ое тело системы со стороны j-го тела системы, F_i – внешняя сила, действующая на i-ое тело системы.

Рассмотрим механическую систему, состоящую из N материальных точек массами m₁, m₂, …, m_N. Предположим, что на каждое из них действуют как тела самой системы, так и внешние, по отношению к ней, тела.

Запишем уравнение второго закона Ньютона для каждого из тел системы:

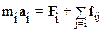, (i=1, 2, …,N).

Сложим почленно правые и левые части уравнений, в результате чего получим

.

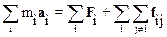Третий закон Ньютона позволяет утверждать, что сумма всех внутренних сил, действующих в системе, равна нулю. Таким образом:

.

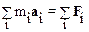Преобразуем полученное соотношение:

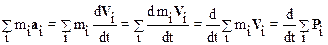
Обозначим 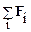через R^ВНЕШ– равнодействующую всех внешних сил, а 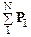какР– импульс системы.

Уравнение (2.30) примет вид:

.

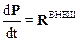Можно сделать следующие выводы.

· Скорость изменения импульса механической системы равна сумме внешних сил, действующих на эту систему.

· Уравнение (2.23), полученное для материальной точки, аналогично уравнению (2.31) справедливому для системы материальных точек и для механической системы.

Замечание.

· Импульс тела, имеющего неподвижную ось вращения, равен нулю.

Это утверждение несложно доказать в общем случае. Проиллюстрируем его примером. Вычислим импульс однородного диска, вращающегося вокруг неподвижной оси, проходящей через его центр.

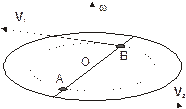
Рис. 2.15

Для этого разделим мысленно диск на элементарные части, так, чтобы массы этих частей были одинаковыми. Рассмотрим две частицы тела dm₁ и dm₂, расположенные в точках А и В диаметра на равных расстояниях и по разные стороны от центра диска (см. рис.2.15).

Линейные скорости этих частиц равны по величине, но противоположны по направлению: V₁= – V₂. Суммарный импульс частиц dm₁ и dm₂ равен нулю, т. к.

dmV₁+dmV₂=dm (V₁+V₂)=0.

Так как каждой частице на диске найдется частица ей диаметрально противоположная, то суммарный импульс диска равен нулю.

Импульс имеет большое значение при рассмотрении процессов соударения, которые будут рассматриваться далее.

· Удар– взаимодействие, протекающее в течение малого промежутка времени.

· Абсолютнонеупругимударомназывается взаимодействие, в результате которого тела начинают двигаться вместе с одинаковыми скоростями. Можно говорить, что при неупругом ударе образуется составное тело с массой, равной массе сталкивающихся тел.

· Абсолютноупругимударомназывается взаимодействие, в результате которого скорости тел изменяются, но суммарные импульс механическая энергия остаются неизменными.