По окружности
Кинематика вращательного движения материальной точки рассматривалась в пунктах 1.4-1.5. Было отмечено, что даже при равномерном движении материальной точки по окружности, ее линейная скорость непрерывно изменяется по направлению. Это происходит благодаря ускорению (см.(1.24)) , называемому центростремительным аЦ, или нормальным ускорением – аn. Ускорение материальной точки, в соответствии со вторым законом Ньютона, сонаправлено с вектором равнодействующей приложенных сил, и равно:
.
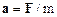Таким образом, равномерное движение по окружности материальная точка может совершать, если равнодействующая F всех сил, приложенных к ней, направлена к центру окружности. Часто силу вызывающую центростремительное ускорение называют "центростремительной силой". Этот термин, как правило, вызывает заблуждение, ориентируя на поиск специфической центростремительной силы. Такой особой – центростремительной силы в природе не существует. Центростремительное ускорение вызывает равнодействующая приложенных сил! Во избежание недоразумений и ошибок мы рекомендуем не пользоваться термином "центростремительная сила", а уравнение динамики вращательного движения материальной точки, масса которой равна m, записывать в следующем виде:
.
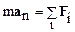Динамика движения материальной точки по окружности может быть изучена на основе общего подхода – с помощью основного закона динамики вращательного движения. Уточним некоторые определения.
· Моментсилыотносительноточки О (полюса О) – векторная физическая величина, равная векторному произведению радиус-вектора r точки приложения силы, проведенного из точки О, и вектора силы F:
.
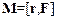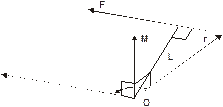
| Рис. 2.16. К определению вектора момента силы. |
Напомним, что векторное произведение представляет собой вектор, направление которого определяется по правилу буравчика (см. (Б.II), параграф 1.5). Абсолютная величина (модуль) вектора векторного произведения равна произведению модулей векторов–сомножителей и синуса угла между ними
.
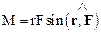Из рисунка 2.16 видно, что модуль М можно представить следующим образом:
,
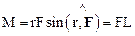где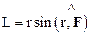 
– плечо силы относительно точки О.
· Плечосилы– кратчайшее расстояние от полюса О до линии действия силы, т. е. длина перпендикуляра, опущенного из полюса на линию действия силы.
· Моментсилыотносительнооси – это скалярная величина М, равная проекции на эту ось вектора момента силы М, определенного относительно точки, лежащей на этой оси:
,
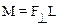где F┴ – проекция силы F на плоскость, перпендикулярную оси Z, L – плечо силы F относительно оси Z.
В случае действия нескольких сил Fi результирующий момент равен векторной сумме моментов Mi всех сил:
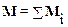или 
,
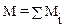в последнем выражении берут алгебраическую сумму, в которой знак Mi зависит от знака проекции Mi на ось Z.
· Моментимпульсаматериальнойточкиотносительноточки (полюса – О) – это векторная величина, равная векторному произведению L=[r,р], где r – радиус-вектор материальной точки (начало которого находится в полюсе О), р – импульс точки.
· Моментинерцииматериальнойточкиотносительнооси – скалярная величина, равная произведению массы m материальной точки на квадрат расстояния r от материальной точки до оси:
.
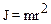Вращательное движение материальной точки описывается уравнением, которое называется основным уравнением динамики вращательного движения. Запишем уравнение второго закон Ньютона для материальной точки, движущейся по окружности радиусом r:
. (*)
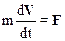Учитывая формулу Эйлера 
, перепишем (*) следующим образом:
.
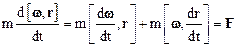Умножим справа обе части полученного уравнения векторно на радиус-вектор r материальной точки:
.
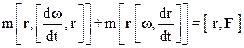Соотношение (2.35) можно упростить. Действительно, поскольку вектор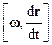 
параллелен вектору r, то
.
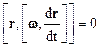Имеем:
.
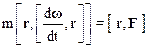Раскрывая оставшееся двойное векторное произведение(см. (1.23)):
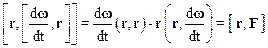
и учитывая, что векторы rиdw/dt взаимно перпендикулярны, а поэтому их скалярное произведение равно нулю, приходим к выражению:
.
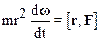Правая часть уравнения (2.36) представляет собой момент М силы Fотносительно полюса.Произведение mr2=J есть момент инерции материальной точки, dw/dt=e – угловое ускорение вращательного движения. Следовательно, уравнение (2.36) можно записать так:
.
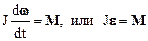Уравнения(2.37) выражает основной закон динамики вращательного движения материальной точки. Оно является не только следствием, но и полным аналогом второго закона Ньютона ma= F для случая поступательного движения материальной точки.
Заметим, что уравнение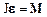 
получено для случая, когда полюс совпадает с центром вращения материальной точки. Если рассматривать движение материальной точки относительно оси вращения Z, то уравнение движения примет соответствующую скалярную форму:
,
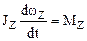где MZ – суммарный момент сил относительно оси Z, JZ – момент инерции относительно оси, wZ – проекция угловой скорости на ось Z, dwZ/dt=e – угловое ускорение.
Продифференцируем уравнение L=[r,P], определяющее момент импульса L материальной точки по времени:
.
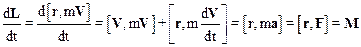Получаем:
.
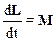Это уравнение является одним из основных уравнений динамики вращательного движения материальной точки. Оно является следствием и аналогом уравнения (2.31) dP/dt=F.
Из соотношения (2.40) следует, что под воздействием приложенного момента сил М¹0 момент импульса материальной точки изменяется таким образом, что
.
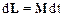Соотношение (2.41) выражает закон изменения момента импульса. Очевидно, что вектор приращения момента импульса dL направлен параллельно вектору М момента силы.
Выражение момента импульса можно представить в следующем виде:
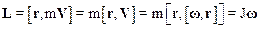
Обратим внимание на то, что соотношения (2.37) и (2.40) получены нами для материальной точки.
Дата добавления: 2015-08-08; просмотров: 822;