Решение задач по динамике движения материальной точки по окружности
Пример 2.4.
Определить угол между вертикальной осью конического маятника и нитью, если тело движется с постоянной угловой скоростью w. Длина невесомой нити подвеса L.
Решение
a=?
w, L, g=9,8 м/с2
|
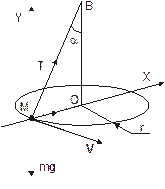
Пусть масса конического маятника равна m. Движение материальной точки происходит в горизонтальной плоскости под действием силы натяжения нити Т и силы тяжести mg(см. рисунок).
Основной закон динамики для данной задачи имеет вид:
ma = Т + mg. (1)
Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Х проходила через центр окружности, а ось Y направим вверх. Проецируя уравнение (1) на оси, имеем:
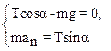 (2)
(2)
Нормальное ускорение материальной точки аn = w2r. Из чертежа следует, что радиус траектории маятника r=ОМ равен r=Lsina, где L=МВ – длина подвеса. Используя дополнительные соотношения, преобразуем уравнения системы (2):
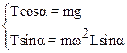 (3)
(3)
Из уравнений (3) следует:
cosa = g/w2L,
или
a = arccos(g/w2L).
Пример 2.5.
На веревке длиной R = 1м висит груз массой m = 5 кг. Максимальное натяжение, которое может выдержать веревка, TMAX = 60 Н. Оборвется ли веревка, если ее отклонить на угол a = 30°? На какой максимальный угол можно отклонить веревку, чтобы она не разорвалась?
| aMAX=? ОА=R=1м, m=5 кг, TMAX=60 H, a=30° | 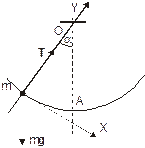
|
Решение.
На груз m действуют две силы: сила тяжести mg и сила натяжения Т. Основной закон динамики принимает вид:
ma = mg + Т. (1)
Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Y проходила через центр окружности, а ось Х направим по касательной.
Проецируя уравнение (1) на оси Y и X имеем:
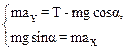 (2)
(2)
Ускорение ах, входящее во второе уравнение системы (2) представляет собой тангенциальное ускорение и указывает, что модуль скорости движущегося тела меняется с течением времени. Сила натяжения Т в точке А определяется первым из уравнений (2):
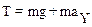 (3)
(3)
Ускорение aY, есть нормальное или центростремительное, ускорение аn. Очевидно, что максимальное натяжение веревка испытывает в точке А, так как в этой точке тело имеет максимальную скорость, а значит – максимальное нормальное ускорение. Используя выражение aY=аn=V2/R для нормального ускорения, преобразуем уравнение (3):
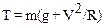 (4)
(4)
Скорость тела в точке А можно определить с помощью закона сохранения механической энергии. В точке наибольшего отклонения полная механическая энергия – это потенциальная энергия еП = mgh, где h = R(1- соsa). В точке А механическая энергия равна кинетической (за нулевой уровень потенциальной энергии удобно принять уровень соответствующий нижней точке А). Уравнение закона сохранения энергии запишем так:
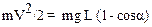 .
.
Откуда получим, что квадрат скорости с точке А равен
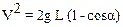 . (5)
. (5)
Подставляя в (4) выражение (5) получим окончательно для силы натяжения:
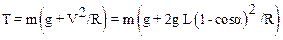 . (6)
. (6)
Подставляя в (6) максимальное значение силы Т=Тmax можно определить угол при котором веревка оборвется, т. к. достигается предельное усилие. Расчеты дают что amax=45°.
Итак, если веревку отклонить на 30°, то она не оборвется.
Пример 2.6.
Тело скатывается с вершины гладкой сферической поверхности радиуса R. Найти, при какой скорости тело оторвется от поверхности. Считать, что трение отсутствует.
Решение.
| H=? R m=0 | 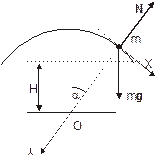
|
На скользящее тело действуют сила тяжести mg и сила N нормальной реакции полусферы. Уравнение движения имеет вид
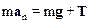 . (1)
. (1)
Направим ось Х по касательной поверхности полусферы, ось Y – радиально в направлении ее центра. Проецируя уравнение (1) на оси получим:
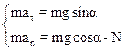
Преобразуем полученные уравнения.
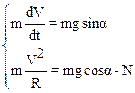 (3)
(3)
Если учесть, что время движения dt может быть вычислено по формуле dt=dℓ/V, где dℓ=Rda, то первое уравнение приводится к следующему виду
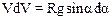 .
.
Интегрируя последнее по V и a, получим соотношение
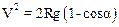 . (4)
. (4)
В момент отрыва тела от полусферы реакция опоры обращается в ноль, и второе из уравнений (3) принимает вид
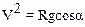 (5)
(5)
исключив a из соотношений (4) и (5) найдем
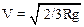 .
.
Пример 2.7.
Найти максимальную разность между силами натяжения нити при вращении в вертикальной плоскости шарика массой m на невесомой нити.
Решение
| (Т1-Т2)МАХ=? m | 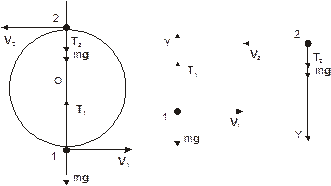
|
На шарик действуют две силы: сила натяжения Т и сила тяжести mg. Уравнение движения (второй закон Ньютона) запишется так:
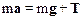 . (1)
. (1)
Для нахождения максимальной разности между силами натяжения, возникающими при вращении шарика, вычислим силы натяжение нити в точках 1 и 2.
Для положения 1 уравнение движения в проекции на оси координат "1" запишется в виде:
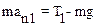 , (2)
, (2)
где 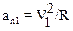 .
.
Аналогично, в положении 2 для проекций в системе координат "2" имеем :
 . (3)
. (3)
так как 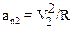 , то из (2) и (3) имеем
, то из (2) и (3) имеем
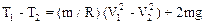 (4)
(4)
Разность 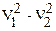 определим из закона сохранения энергии. Если выбрать за нулевой уровень отсчета потенциальной энергии уровень точки 1, то можно записать, что
определим из закона сохранения энергии. Если выбрать за нулевой уровень отсчета потенциальной энергии уровень точки 1, то можно записать, что
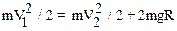 .
.
Следовательно,
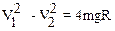 . (5)
. (5)
Подставляя (5) в соотношение (4) имеем окончательно
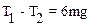 .
.
Пример 2.8.
Вал в виде сплошного цилиндра массой m=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m1=2 кг. С каким ускорением a будет опускаться гиря, если её предоставить самой себе.
a=?
m=10 кг, m1=2 кг
Решение
В задаче участвуют два тела, совершающие различные движения: тело m1 движется прямолинейно, вал – вращается. Уравнения движения имеют следующий вид:
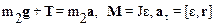 , (1)
, (1)
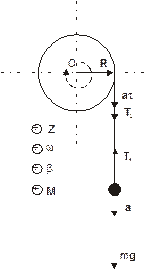
в системе уравнений (1) введены обозначения: аt – тангенциальное ускорение точек на периферии вала, Т – сила натяжения шнура, r – радиус вала, М – момент, вращающий вал, а – ускорение тела m1.
|
Момент, вращающий вал равен 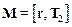 , J – момент инерции вала относительно геометрической оси. Рассматривая вал как однородный цилиндр, считаем, что его момент инерции равен J = 1/2m1r2.
, J – момент инерции вала относительно геометрической оси. Рассматривая вал как однородный цилиндр, считаем, что его момент инерции равен J = 1/2m1r2.
Определим направление векторных величин (по правилу буравчика) и выбрав направление осей координат как показано на рисунке запишем систему (1) в проекциях.
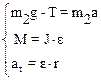 (2)
(2)
При условии, что шнур нерастяжим и отсутствует его скольжение по поверхности вала тангенциальное ускорение аt по модулю равно поступательному ускорению а груза m1: аt=а. С учетом дополнительных соотношений уравнения системы (1) примут вид:
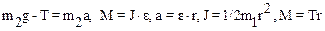 (3) Решая систему относительно ускорения a получим:
(3) Решая систему относительно ускорения a получим:
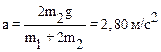 .
.
Пример 11.
Через блок в виде диска, имеющий массу m=80г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100г и m2=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Решение.
| а1, а2=? m=80 г=8×10–2 кг m1=100 г =10–1 кг m2=200 г=2×10–1 кг | 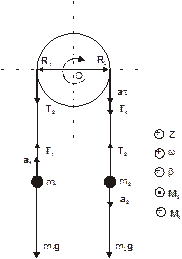
|
Рассматриваемая в задаче система состоит из двух движущихся поступательно грузов и одного вращающегося диска. На каждый из грузов действует две силы: сила тяжести mg, направленная вниз, и сила Т натяжения нити, направленная вверх. Запишем законы поступательного и вращательного движения этих тел.
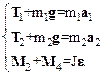 (1)
(1)
Результирующий вращающий момент, приложенный к диску, равен
М=М2+М4=[R1,T2]+[R2,T4],
R1 и R2 – радиус-векторы точек приложения сил натяжения нити T2 и T4. Предположим, что m2 > m1, поэтому ускорения грузов будет направлено, как показано на рисунке. Выберем произвольное направление осей координат (например, как на рисунке) и запишем систему уравнений в проекциях.
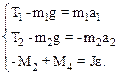 (2)
(2)
При условии, что нить нерастяжима, отсутствует ее скольжение по поверхности диска, тангенциальное ускорение точек на поверхности диска аt по модулю равно поступательному ускорению а грузов: аt=а. Угловое ускорение диска связано с линейным ускорением грузов соотношением 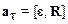 ; в скалярной форме
; в скалярной форме 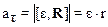 . Пренебрегая массой нити приходим к выводу, что силы натяжения Т1 и Т2 равны по величине. Учтем также, что момент инерции диска J = mr2/2. С учетом приведенных дополнительных соотношений система (2) принимает вид:
. Пренебрегая массой нити приходим к выводу, что силы натяжения Т1 и Т2 равны по величине. Учтем также, что момент инерции диска J = mr2/2. С учетом приведенных дополнительных соотношений система (2) принимает вид:
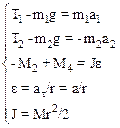
Решая полученную систему, получим
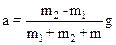 .
.
После подстановки числовых значений имеем
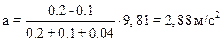
Дата добавления: 2015-08-08; просмотров: 3934;
