Задачи к главе 2 для самостоятельного решения

2.1. Определить, на каком расстоянии от поверхности Земли должен находиться спутник, если он вращается в плоскости экватора с периодом, равным периоду вращения Земли вокруг оси.

35870 км.

2.2. Какова должна быть продолжительность суток на Земле, чтобы тела, находящиеся на экваторе, были невесомы.

1,41 часа.

2.3. Тело массой 1 кг, закрепленное на конце невесомого стержня длиной 0,5 м, вращается в вертикальной плоскости в поле силы тяжести с постоянной частотой 0,2Гц. Вычислить разность сил, действующих на стержень в нижнем и верхнем положении.

1,6 Н.

2.4. Камень массой 0,5 кг, привязанный к веревке длиной 50 см, вращается в вертикальной плоскости. Сила натяжения веревки в нижней точке окружности равна 44 Н. На какую высоту поднимется камень, если веревка отрывается в тот момент, когда его скорость направлена вертикально вверх?

2 м.

2.5. Определить плотность планеты, если тела на ее экваторе невесомы. Период обращения планеты вокруг оси – Т = 20 ч.

r = 27, 25кг/м3.

2.6. Определить максимальную силу натяжения, которую выдерживает нить, к концу которой привязан шарик массой m = 500 г, если она разрывается, когда ее отклоняют на угол, больший 60°.

Т = 9,8Н.

2.7. На горизонтально вращающемся диске на расстоянии 1 м от вертикальной оси вращения лежит груз. При каком числе n оборотов в секунду груз начнет скользить, если коэффициент трения между грузом и диском 0,01?

n = 0,05 об/с.

2.8. Маленький шарик массы m, подвешенный на невесомой нити, отклоняют от положения равновесия на угол a = 60° и отпускают. Определить натяжение нити в начальный момент движения.

Т = mg/2.

2.9. В конусе лежит шарик. Конус начинают вращать с угловой скоростью w. На каком расстоянии от вершины конуса шарик будет находиться в состоянии равновесия? Угол раствора конуса равен 2a.

L=g/(w2cosa).

2.10. Два тела массами m₁ и m₂ находятся на стержне, по которому они могут свободно двигаться. Тела соединены нитью длиной L. Стержень вращается с угловой скоростью w относительно вертикальной оси вращения. Определить, на каком расстоянии от оси вращения установятся тела.

x₁ = m₁L/(m₁ + m₂), x₂ = m₂L/(m₁ + m₂).

2.11. Радиус планеты Марс составляет 0,53 радиуса Земли, а плотность - 0,74 плотности Земли. Найти ускорение свободного падения на Марсе.

3,86 м/с².

2.12. Найти линейную скорость и период обращения искусственного спутника Земли по круговой орбите на расстоянии Н=R от поверхности Земли, где R = 6400 км - радиус Земли. Ускорение свободного падения на поверхности Земли принять равным 9,8м/с².

v = 5, б км/с; Т = 4 ч.

2.13. Пуля попадает в шар массой М, висящий на нити длиной L, и застревает в нем. С какой максимальной скоростью может лететь пуля, чтобы нить не оборвалась? Максимальная сила натяжения, которую выдерживает нить, равна F_MAX, масса пули m₀.

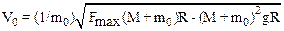
2.14. Определить угловую скорость w вращения двойной звездной системы. Массы звезд М₁ и М₂, расстояние между их центрами R. Найти также ускорения, с которыми движутся звезды.

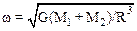; a₁ = GМ₂ / R²; a₂ = GМ₁ / R².

2.15. Найти первую космическую скорость на планете, масса которой в 3 раза, а радиус в 2 раза больше, чем у Земли. Принять первую космическую скорость на Земле равной 8×10³ м/с.

9,8×10³ м/с.

2.16. Найти момент инерции: а) тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня m и длина L; б) тонкой однородной прямоугольной пластинки относительно оси, проходящей через одну из вершин пластинки перпендикулярно к ее плоскости, если стороны пластинки раны a и b, а ее масса равна m.

а) I = mL²/3; б) I = m(a²+b²)/3.

2.17. Тонкая однородная пластинка массы m=0,60 кг имеет форму равнобедренного прямоугольного треугольника. Найти ее момент инерции относительно оси, совпадающей с одним из катетов, длина которого а=200 мм.

I=ma²/6=4,0 г·м².

2.18. Вычислить момент инерции: а) медного однородного диска относительно оси симметрии, перпендикулярной к плоскости диска, если его толщина b=2,0 мм и радиус R=100 мм; б) однородного сплошного конуса относительно его оси симметрии, если масса конуса m и радиус его основания R.

а) I = πρbR⁴/2=2,8 г·м²; б) I = 0,3mR².

2.19. Найти момент инерции тонкого проволочного кольца радиусом R и массы m относительно оси, совпадающей с его диаметром.

I=mR²/2.

2.20. Однородный диск радиуса R имеет круглый вырез (рис. 1). Масса оставшейся части диска равна m. Найти момент инерции такого диска относительно оси, перпендикулярной к плоскости диска и проходящей: а) через точку О, б) через его центр масс.

а) I_O = (13/24)mR²; б) I_C=(37/72)mR².

2.21. На ступенчатый блок (рис. 2) намотаны в противоположных направлениях две нити. На конец одной нити действуют постоянной силой F, а к концу другой нити прикреплен груз массы m. Известны радиусы R₁ и R₂ блока и его момент инерции I относительно оси вращения. Трения нет. Найти угловое ускорение блока.

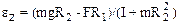
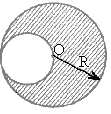Рис 1.

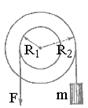Рис. 2

2.22. Человек массой m₁ стоит на краю горизонтального однородного диска массой m₂ и радиусом R, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент человек начал двигаться по краю диска, совершил перемещение на угол 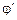относительно диска и остановился. Пренебрегая размерами человека, найти угол, на который повернулся диск к моменту остановки человека.

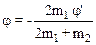
2.23. Два горизонтальных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны I₁ и I₂, а угловые скорости – w₁ и w₂. После падения верхнего диска на нижний оба диска благодаря трению между ними начали через некоторое время вращаться как единое целое. Найти: а) установившуюся угловую скорость вращения дисков; б) работу, которую совершили при этом силы трения.

а) ω=(I₁ω₁+I₂ω₂)/(I₁+I₂),

б) А = - [I₁I₂/2(I₁+I₂)](ω₁ -ω₂)².

2.24. На горизонтальную ось насажены маховик и легкий шкив радиусом R=5см. На шкив намотан шнур, к которому привязан груз массой m=0,4кг. Опускаясь равноускоренно, груз прошел путь s=1,8м за время t=3с. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой.

2.25. Вал массой m=100кг и радиусом R=5см вращался с частотой n=8c^-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F=40Н, под действием которой вал остановился через t=10с. Определить коэффициент трения f.

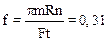
2.26. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение а оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.

1) a=2g/3; 2) a=g/2.

2.27. Человек стоит на скамье Жуковского и ловит рукой мяч массой m=0.4кг, летящий в горизонтальном направлении со скоростью V=20м/с. Траектория мяча проходит на расстоянии r=0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью w начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6кг·м².

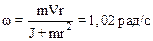
2.28. На краю горизонтальной платформы, имеющий форму диска радиусом R=2м, стоит человек массой m₁=80кг. Масса m₂ платформы равна 240кг. Платформа может вращаться вокруг вертикальной оси, проходящий через ее центр. Пренебрегая трением, найти, с какой угловой скоростью w будет вращаться платформа, если человек будет идти вдоль ее края со скоростью V=2м/с относительно платформы.

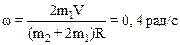
2.29.В центре скамьи Жуковского стоит человек и держит в руках стержень длиной L=2,4 м и массой m=8 кг, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с частотой n₁=1 с^-1. С какой частотой n₂ будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции J человека и скамьи равен 6 кг·м².

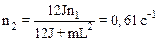
2.30. Чему равен момент инерции тонкого прямого стержня длиной 0,5 м и массой 0,2 кг относительно оси, перпендикулярной к его длине и проходящей через точку стержня, которая удалена на 0,15 м от одного из его концов?

6·10^-2 кг·м².

2.31. На барабан радиусом R=10 см намотана нить, к концу которой привязан груз массой m= 0,50 кг. Найти момент инерции барабана, если груз опускается с ускорением а =1,0 м/с².

I=mR²(g-a)/a=4,4·10^-2 кг·м².

2.32. Через блок, масса которого m=100 г, перекинута тон­кая гибкая нерастяжимая нить, к концам которой подвешены два груза массами m₁=200г и m₂=300 г. Грузы удерживаются в неподвижном положении. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Чему равно угловое ускорение блока, если его радиус 10 см? Трением пренебречь.

a=(m₂-m₁)g/(m₁+m₂+m/2)=1,8 м/с²; ε=(m₂-m₁)g/(m₁+m₂+m/2)R=18 с^-2.

2.33. Из колодца с помощью ворота поднималось ведро с водой массой m=10 кг. В момент, когда ведро находилось на высоте h=5,0 м от поверхности воды, рукоятка освободилась, и ведро стало двигаться вниз. Определить линейную скорость рукоятки в момент удара ведра о поверхность воды в колодце, если радиус рукоятки R=30 см, радиус вала ворота r =10 см, его масса m₁=20 кг. Трением и массой троса, на котором подвешено ведро, пренебречь.

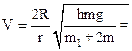21 м/с.

2.34. Маховик массой m₁=l,0 кг укреплен на шкиве радиусом r=5,0 см и массой m₂=200 г, который приводится во вращение с помощью опускающейся гири массой m₃=500 г, привя­занной к концу намотанной на шкив веревки. Через какое время скорость маховика достигнет n=5,0 об/с? Считать, что вся масса маховика распределена по его ободу радиусом R=40 см.