Глава 3. Статика

· Статика– это раздел механики, посвященный изучению условий равновесия механической системы, а так же отдельного тела.

Пусть тело в начальный момент времени покоится, т. е. его начальная линейная скорость V₀ и начальная угловая скорость w₀ равны нулю. Условия, при которых тело и в последующие моменты времени будет находиться в равновесии (в покое), следуют из второго закона Ньютона и уравнения моментов:

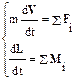
Действительно, V=V₀=0 если dV/dt=a=0 и поступательное движение не начнется. Аналогично момент импульса L=L₀ останется равным нулю при отсутствии углового ускорения. Эти условия выполнены, если равнодействующая приложенных сил равна нулю и суммарный момент сил равен нулю:

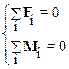
Уравнения (3.2) называются условиями равновесия механической системы (тела). Для материальной точки в качестве условий равновесия могут выступать первое уравнение системы. Система (3.2) двух векторных уравнения соответствуют следующей системе шести скалярных уравнений для проекций сил и моментов сил, действующих на материальную систему:

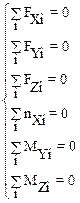
При исследовании равновесия положение осей X, Y, Z можно выбрать произвольно. Удобно провести их через центр масс тела.

· Центроммасс (центроминерции) системы называют воображаемую точку, радиус – вектор которой определяется следующим образом:

,

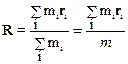здесь m_i и r_i – масса и радиус-вектор i-ой частицы системы (тела) в некоторой системе отсчета, 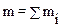– масса системы.

Дифференцируя (3.4) легко получить, что импульс Р системы равен произведению ее массы на скорость V_c движения центра масс:

.

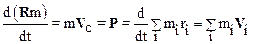Используя соотношение (3.5) и уравнение второго закона Ньютона dP/dt=F^внеш запишем

.

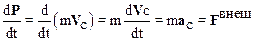Таким образом, приходим к теоремео движении центра масс системы:

· центр масс системы движется, как материальная точка с массой равной массе системы, к которой приложена равнодействующая сил.

Уравнение для моментов 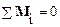может быть написано для произвольного полюса. Можно показать, что при условии 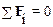величина результирующего момента сил не зависит от выбора полюса.

Найдем суммарный момент сил тяжести, действующих на все частицы системы (тела), относительно произвольной точки О:

,

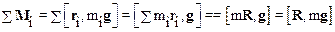где 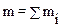– масса тела, R -радиус-вектор центра масс тела. Таким образом, момент сил тяжести частиц тела относительно произвольной точки О равен моменту силы тяжести тела mg, приложенной к центру масс тела. Из формулы (3.7) следует, что суммарный момент сил тяжести относительно центра масс тела равен нулю (так как радиус-вектор центра масс R= 0).