В механике

Все силы в механике делятся на консервативные и неконсервативные. Такое деление связано с понятием "потенциальная энергия", которое рассматривается далее. В связи с этим, консервативные силы являются потенциальными, а неконсервативные – не потенциальными.

· Консервативнымисиламиназывают силы, работа которых не зависит от формы траектории, а только от начального и конечного положения движущейся материальной точки, к которой они приложены.

Консервативные силы зависят от взаимного расположения материальных точек (тел) системы, т. е. от ее конфигурации, а также от положения системы во внешних силовых полях. Отметим сразу, что в механике рассматриваются следующие консервативные силы: сила всемирного тяготения, сила тяжести и упругости. К консервативным силам относят также силу Кулона, описывающую взаимодействие заряженных частиц.

· Все силы, которые не являются консервативными, например, диссипативные и гироскопические силы, относят к неконсервативным силам.

· Диссипативными[4] силаминазывают силы, полная работа которых в замкнутой системе всегда отрицательна.

Диссипативные силы зависят не только от взаимного расположения взаимодействующих тел, но и от их относительной скорости. К ним, например, относятся сила трения скольжения, сила сопротивления движению в жидкой или газовой среде. Направление диссипативных сил всегда противоположно направлению относительной скорости взаимодействующих тел. В разделе будет показано, что, в самом общем случае, механическая энергия системы может не сохраняться. Одна из причин этого заключается в действии диссипативных сил, которые приводят к частичному или полному переходу механической энергии во внутреннюю энергию.

· Гироскопическимисиламиназывают силы, которые действуют перпендикулярно скорости движения частицы (тела) и зависят от ее величины.

Гироскопической силой является, например, сила Лоренца 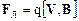. В силу специфической направленности гироскопических сил они не совершают работы, не изменяют модуль скорости, а только изменяют ее направление. Действительно, вектор векторного произведения 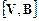перпендикулярен V, поэтому:

.

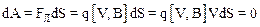Возвращаясь к изучению свойств консервативных сил, докажем их основное свойство:

· работа консервативных сил по любой замкнутой траектории равна нулю.

Пусть материальная точка (система) из положения 1 перешла в положение 2 по траектории 132 (см. рис. 4.3).

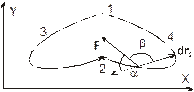
Рис. 4.3. Свойство консервативных сил

При этом консервативной силой F, действующей на нее, была совершена работа 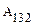. Предположим, что при переходе в положение 2 по траектории 142, работа равна 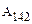. По определению консервативных сил имеем 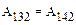. Заметим теперь, что работы, совершенные на участках 142 ( 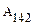) и 241 ( 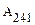) отличаются знаком: т. е. 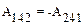. Это связано с тем, что на каждом элементарном участке траектории 241 угол b между вектором F и вектором перемещения dr₂=dr₂₄₁ является дополнительным к углу a между векторами F и вектору dr₁=dr₁₄₂, который противоположен вектору dr₂. По этой причине знак функции косинуса (и работы) в выражении (4.1) изменяется на противоположный.

На основании (4.5) заключаем, что работа консервативных сил по замкнутой траектории 13241 А₁₃₂₄₁ равна сумме работ А₁₃₂ и А₂₄₁ вдоль траекторий 132 и 241, соответственно:

А₁₃₂₄₁= А₁₃₂+ А₂₄₁= А₁₃₂– 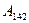=0.

Сформулированное утверждение доказано.