Работасилы всемирного тяготения

Вычислим работу, совершаемую силой всемирного тяготения со стороны тела массой М при перемещении тела массой m из положения, характеризуемого радиус-вектором r₁ в положение с радиус-вектором r₂ (см. рис. 4.5).

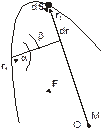
Рис. 4.5. Вычисление работы силы тяготения и силы упругости. Тяготеющая масса М расположена в точке О

Гравитационное поле является центральным, поскольку сила тяготения действует вдоль линии соединяющей материальную точку m (или центр масс этого тела) с центром О поля тяготения. По определению работы (4.2) имеем:

,

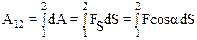где сила F определяется законом (2.12).

Из рисунка видно, что dScosa=dr, поэтому dA=F(r)dr, и для А₁₂ имеем:

.

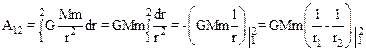Полученное выражение не содержит сведений о траектории движения тела, и можно утверждать, что работа центральной силы зависит только от начального и конечного расстояния r₁ и r₂ движущейся точки до силового центра.