Потенциальная энергия. Пусть на материальную точку или механическую систему действуют только консервативные и гироскопические силы
Пусть на материальную точку или механическую систему действуют только консервативные и гироскопические силы, не зависящие от времени. Говоря иначе, материальная точка находится в стационарном поле сил. Примем условно за нулевое какое-либо состояние системы. Рассматривая иные состояния, назовем потенциальной энергией системы в некотором ином состоянии величину U, равную работе консервативных сил, совершаемой при переводе системы из этого состояния в нулевое.
· Потенциальнойэнергиейсистемы в некотором состоянии называют скалярную величину U, равную работе консервативных сил совершаемой при переводе системы из этого состояния в состояние, условно принятое за нулевое.
Поскольку работа консервативных сил не зависит от траектории движения материальной точки, то ее потенциальная энергия зависит только от начального состояния системы. Это означает, что потенциальная энергия системы определяется ее состоянием. Возможность произвольно выбрать нулевое состояние (нулевого уровня потенциальной энергии) означает, что потенциальная энергия системы определяется не однозначно, а с точностью до произвольной постоянной С, зависящей от сделанного выбора. Действительно, если за нулевое состояние условно принять состояние, изображаемое точкой О (см. рис.5.1), то потенциальная энергия UМ системы, находящейся в состоянии, изображаемом точкой M, равна работе АМО, совершенной силами поля при переходе из состояния М в состояние О.
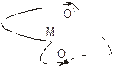
| Рис. 5.1. К определению потенциальной энергии |
Если принять за начальное точку ОI, то потенциальная энергия точки М будет равна работе 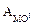 по перемещению из М в ОI. Вследствие консервативности сил поля работа по траектории МО равна работе по траектории МОIО:
по перемещению из М в ОI. Вследствие консервативности сил поля работа по траектории МО равна работе по траектории МОIО:
АМО= 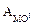 +
+ 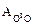 .
.
Заметим, что работа 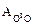 вполне определенная величина, зависящая только от выбора точек О и ОI. Таким образом, при изменении положения начальной точки О потенциальная энергия изменяется на постоянную величину:
вполне определенная величина, зависящая только от выбора точек О и ОI. Таким образом, при изменении положения начальной точки О потенциальная энергия изменяется на постоянную величину:
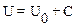 .
.
Из сказанного выше следует, что потенциальная энергия в положении О равна нулю. Однако ее можно считать равной не нулю, а некоторому произвольному значению. Тогда, при переходе системы из состояния М в нулевое, необходимо говорить не о потенциальной энергии состояния М, а о разности потенциальных энергий в состоянии М и О. Произвол в выборе постоянной C не влияет ни на теоретические выводы, ни, тем более, на ход физических процессов. Существенной оказывается не абсолютная величина потенциальной энергии U, а ее изменение – 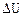 , которое не содержит произвольной постоянной С.
, которое не содержит произвольной постоянной С.
Пусть система перешла из состояния M в состояние N. Работу AMN, совершенную при этом консервативными силами, можно выразить через потенциальные энергии состояний M и N.

| Рис. 5.2. К определению величины потенциальной энергии |
Пусть (см. рис. 5.2) этот переход осуществлен через точку О, по траектории MON. Тогда AMN=AMON=AMO+AON. По определению потенциальной энергии можно записать: UM=AMO+C, UN= ANO+C, где С – одна и та же постоянная. Имеем:
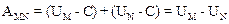 .
.
Разность потенциальных энергии начального и конечного состояний UM-UN представляет собой ее убыль (убыль равна приращению, взятому с противоположным знаком). Полученное соотношение играет важную роль: оно позволяет утверждать, что:
· работа консервативных сил, действующих на тела механической системы равна убыли потенциальной энергии системы:
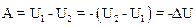 .
.
Конкретный вид функции U, определяющей величину потенциальной энергии зависит от характера действующих сил, или от природы силового поля. В разделах 4.1.1 – 4.1.3 получены выражения для работы консервативных сил различной природы. Сравнивая соотношения (4.11), (4.12) и (4.13) с соотношением (5.1) легко придти к выводу, что потенциальная энергия:
· в поле силы тяжести определяется соотношением
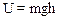
· в поле силы упругости определяется соотношением
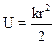 .
.
Определение потенциальной энергии в поле силы всемирного тяготения имеет особенность. Соотношение (4.12) получено непосредственным вычислением работы силы всемирного тяготения:
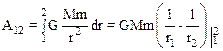
Как правило, тела считают равной нулю. Это оправдано тем, что на бесконечно большом расстоянии (r2=¥) сила тяготения обращается в ноль и энергия взаимодействия отсутствует, т. е. U¥=0. Из формулы (4.17) следует, что А1¥=-DU=U¥-U1.
· Итак, имеем для потенциальной энергии в поле тяготения соотношение
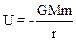
Дата добавления: 2015-08-08; просмотров: 939;
