Потенциальная энергия и сила поля. Зная силы, действующие на частицы механической системы, можно определить величину ее потенциальной энергии
Зная силы, действующие на частицы механической системы, можно определить величину ее потенциальной энергии. Для основных сил, рассматриваемых в механике, соответствующие расчеты были проведены в пункте 4.1. Можно решить обратную задачу: по величине потенциальной энергии определить величину действующей консервативной силы. Рассмотрим материальную точку m, находящуюся в поле консервативных сил. Очевидно, ее потенциальная энергия зависит от положения, т. е. от координат материальной точки: U=U(X,Y,Z). Предположим, что материальная точка m совершила бесконечно малое перемещение dS. Сила, действующая на нее, совершила при этом элементарную работу dA. Известно (5.1), что работа консервативных сил равна убыли потенциальной энергии, т. е.:
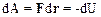 .
.
Для определения вектора силы достаточно определить его проекции на оси прямоугольной системы координат. Уравнение (5.6) можно записать так
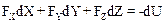 .
.
С другой стороны, дифференциал dU функции U равен:
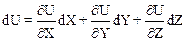 .
.
Сравнивая коэффициенты при dX, dY и dZ в последних соотношениях, приходим к выводу, что проекции вектора силы на оси координат равны первым производным потенциальной энергии, взятым с противоположным знаком:
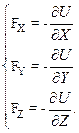
Соотношения (5.9) принято записывать в векторной форме следующим образом:
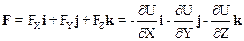 ,
,
или иначе, с использованием градиента – векторного оператора Гамильтона
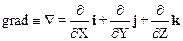 .
.
Так:
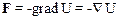 .
.
Дата добавления: 2015-08-08; просмотров: 760;
