Кинетическая энергиявращательного движения
Найдем кинетическую энергию тела, вращающегося относительно неподвижной оси. Будем рассматривать тело как систему материальных точек и воспользуемся формулой (5.15). Скорость Vi материальной точки выразим через угловую скорость вращения тела по формуле Эйлера (1.21).
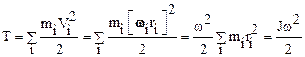 .
.
Здесь через ri обозначен радиус-вектор i-ой частицы тела, wi ее угловая скорость (одна и таже для всех точек), наконец J – момент инерции тела относительно оси, проходящей через его центр масс. Таким образом, кинетическая энергия вращающегося тела описывается следующей формулой
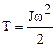 .
.
Последнее уравнение для вращательного движения тела аналогично уравнению T=mV2/2 для поступательного движения.
Если тело движется поступательно в инерциальной системе отсчета со скоростью V0 и вращается относительно подвижной оси, проходящей через центр масс с угловой скоростью w, причем ось перпендикулярна направлению скорости V0 (так называемое плоское движение, например, качение колеса), то его кинетическая энергия Т равна сумме кинетических энергий поступательного и вращательного движений:
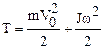 ,
,
здесь m – масса тела, J – его момент инерции относительно оси вращения.
Докажем справедливость соотношения (5.17). Воспользуемся классическим законом сложения скоростей:
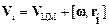 ,
,
где 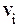 - скорость движения i-й материальной точки относительно неподвижной системы отсчёта; VЦМ – скорость центра масс тела; ri – радиус-вектор i-й точки, проведенный из центра масс; w – угловая скорость вращения тела. Возведя выражение для
- скорость движения i-й материальной точки относительно неподвижной системы отсчёта; VЦМ – скорость центра масс тела; ri – радиус-вектор i-й точки, проведенный из центра масс; w – угловая скорость вращения тела. Возведя выражение для 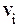 в квадрат, получим:
в квадрат, получим:
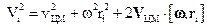 .
.
Используем свойство аддитивности кинетической энергии, и запишем:
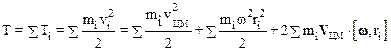 .
.
В полученном выражении последнее слагаемое равно нулю, т. к.
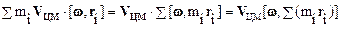 ,
,
вектор 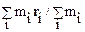 по определению равен радиус-вектору центра масс тела, который равен нулю в системе центра масс. Окончательно имеем:
по определению равен радиус-вектору центра масс тела, который равен нулю в системе центра масс. Окончательно имеем:
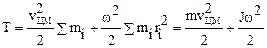 .
.
Дата добавления: 2015-08-08; просмотров: 853;
