Закон сохранения механической энергии

Если на материальную точку (тело) действует сила, то ее (его) кинетическая энергия не остается постоянной. Интегрируя соотношение (5.12), получим, что

.

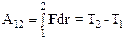Физический смысл полученной формулы

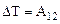
заключается в следующем:

· приращение кинетической энергии материальной точки равно работе равнодействующей сил, приложенных к ней.

6.3.1. Механическая энергия материальной точки

(тела) под воздействием консервативной силы

Работа консервативной силы при перемещении материальной точки (тела) из положения 1 в положение 2 – А₁₂ может быть представлена (см. (5.1)) как убыль потенциальной энергии

.

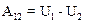Соотношение (6.4), в свою очередь, указывает, что в результате совершения работы увеличивается кинетическая энергия. Сравнивая (5.1) и (6.4) приходим к выводу, что:

,

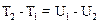или собирая члены, соответствующие одному состоянию в различных частях уравнения:

.

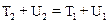Полученный результат означает, что величина полной механической энергии частицы (тела) E=T+U для в поле консервативных сил остается постоянной.

· При отсутствии неконсервативных сил полная механическая энергия остается постоянной – сохраняется.

· Увеличение кинетической энергии системы в присутствии консервативных сил происходит за счет убыли ее потенциальной энергии. Наоборот, уменьшению кинетической энергии системы в присутствии консервативных сил соответствует увеличение ее потенциальной энергии.