Механическая энергия системы

A. Рассмотрим механическую систему, состоящую из n невзаимодействующих частиц, находящуюся в поле консервативных сил. Каждая из этих частиц обладает потенциальной U_i и кинетической T_i энергией. Для каждой частицы системы справедливо утверждение

.

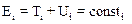Суммируя эти равенства по всем частицам получим

.

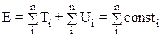Соотношение (6.11) показывает, что полная механическая энергия системы невзаимодействующих между собой частиц в поле консервативных сил является аддитивной величиной. Наконец, из него следует закон сохранения энергии:

· полная механическая энергия системы невзаимодействующих между собой частиц, на которые действуют только консервативные силы, остается постоянной.

B. Рассмотрим, теперь, механическую систему, состоящую из n частиц, на которые могут действовать как консервативные F, так и неконсервативные F* силы. Каждая из этих частиц обладает потенциальной U_i и кинетической T_i энергией. Для i-ой частицы такой системы справедливо утверждение (6.9): при переходе из состояния 1 в состояние 2 изменение полной механической энергии этой частицы равно работе неконсервативных сил:

,

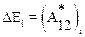здесь 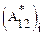– работа неконсервативной силы, действующей на i-ю частицу.

Суммируя аналогичные равенства для всех частиц системы получим

.

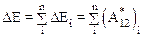С. Рассмотрим, наконец, общий случай механической системы, состоящей из n взаимодействующих между собой частиц. Предположим, что величина внутренних сил f_ij зависит только от взаимного расстояния между частицами. Такие силы являются консервативными. Предположим также, что на частицы системы действуют внешние консервативные F_iи внешние неконсервативные F_i* силы.

Уравнение второго закона Ньютона для i-ой частицы имеет вид:

.

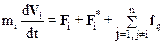Умножая это уравнение скалярно на элементарное перемещение частицы dr_i=V_idt, получим

.

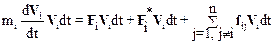Если записать аналогичные уравнения для всех частиц системы и сложить их, то придем к выражению

.

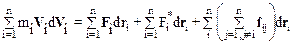Выясним смысл всех членов уравнения (6.13). Левая часть уравнения 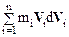в соответствии с (5.12) представляет собой приращение dT кинетической энергии системы. Член 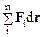согласно (5.1) равен убыли потенциальной энергии –dU_внешн системы во внешнем поле. Член 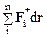равен работе 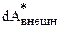внешних неконсервативных сил. Наконец, как следует из соотношений (4.4), (5.1), последний член в (6.13) 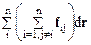равен убыли потенциальной энергии –dU_вз взаимодействия частиц. Таким образом, формулу (6.13) можно записать так:

,

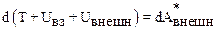где 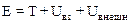– полная механическая энергия системы. Соотношение (6.14) позволяет дать следующую формулировку закона сохранения энергии:

· полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной.

Обратимся вновь к формуле (6.14), которая показывает, что механическая энергия системы может измениться только за счет работы неконсервативных сил. Это замечание позволяет дать еще одну формулировку закона сохранения энергии:

· если отсутствуют неконсервативные силы или они таковы, что не совершают работы в течение некоторого промежутка времени, то полная механическая энергия системы, находящейся в стационарном поле консервативных сил, остается постоянной в течение этого промежутка времени.

Уравнения (6.6), (6.11) и (6.14) это различные выражения закона сохранения полной механической энергии системы.