Глава 7. Динамика малых колебаний
Теория малых колебаний может быть рассмотрена на основании энергетических соотношений. Рассмотрим одномерную механическую систему, находящуюся в стационарном поле консервативных сил. Очевидно, что в этом случае система обладает потенциальной энергией U, которая является функцией одной координаты Х: U=U(Х). Предположим, что зависимость потенциальной энергии от координаты имеет вид, представленный на рисунке 7.1.
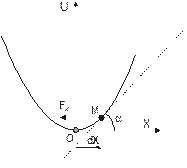
| Рис. 7.1. Зависимость U(X) типа "потенциальной ямы" |
Поместим начало одномерной системы координат в точку, соответствующую минимуму потенциальной энергии UМИН = U(0). Минимальное значение энергии можно положить равным нулю, т. к. потенциальная энергия, в общем случае, определена с точностью до произвольной постоянной.
Предположим, что материальная точка М совершила перемещение dХ из начала координат в положительном направлении оси Х. При этом ее потенциальная энергия стала равна U(X). Разложим функцию U(X) в ряд Маклорена в окрестности точки Х = 0 и пренебрежем малыми членами степени выше второй по dX:
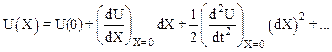
Поскольку при Х=0 потенциальная энергия имеет минимум, то dU/dX = 0; кроме того, U(0) = 0, поэтому из (7.1) следует, что
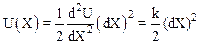 ,
,
где (d2U/dX2)Х=0 = k>0, т. к. дифференцируемая функция имеет минимум в точке Х = 0.
Последнее соотношение позволяет найти силу, действующую на материальную точку М. В соответствии с (5.11):
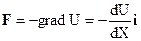 ,
,
поэтому проекция F на ось Х равна
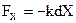 .
.
Силу, пропорциональную смещению (подчиняющуюся) закону Гука (2.20), независимо от ее физической природы, называют упругой. Знак минус в предыдущих формулах означает, что проекция FX отрицательна, т. е. она направлена к положению равновесия. Силу, обладающую такими двумя свойствами, называют возвращающей или восстанавливающей силой.
Заметим, что в выбранной системе координат (см. рис. 7.1) dX = X, поэтому в соответствии со вторым законом Ньютона
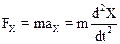
имеем уравнение движения материальной точки в потенциальной яме:
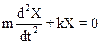 .
.
Несложно проверить подстановкой, что решением этого уравнения является функция вида
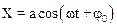 .
.
Это означает, (сравните с (1.33)), что движение материальной тачки носит колебательный характер, причем частота колебаний равна
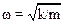 .
.
Очевидно, что периодпружинного маятника равен
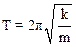 .
.
Запишем некоторые важные энергетические соотношения. Как следует из (7.2) потенциальная энергия колеблющегося тела может быть найдена по формуле, аналогичной формуле для потенциальной энергии деформированной пружины:
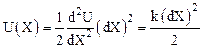 ,
,
кинетическая – по известной формуле:
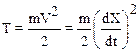 .
.
При отсутствии трения, или другой диссипативной силы, полная энергия Е колебательной системы остается постоянной:
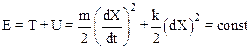 .
.
Используя уравнение для смещения (1.33) в колебательном процессе, запишем выражения (7.3) и (7.4) для энергий следующим образом:
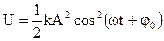 и
и 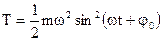 .
.
Наконец, формулы для энергий U и Т можно представить в виде:
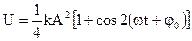 ,
,
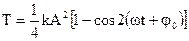 ,
,
откуда следует, что потенциальная (и кинетическая) энергия совершает гармоническое колебание с удвоенной, по сравнению с циклической частотой колебаний, частотой 2w.
В общем случае движение системы принято описывать при помощи обобщенных координат, число которых соответствует числу степеней свободы системы.
Дополнения.
· Числостепеней свободы – число независимых координат, однозначно определяющих положение объекта в пространстве.
В одномерном случае, для описания движения материальной точки достаточно одной обобщенной координаты, роль которой может выполнять также обычная декартова координата Х. Обозначим обобщенную координату через q. Первую производную от обобщенной координаты q по времени t – dq/dt называют обобщенной скоростью.
Если полную энергию колебательной системы можно представить в виде
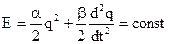 ,
,
то циклическую частоту колебаний системы можно вычислять по формуле:
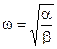 .
.
Дата добавления: 2015-08-08; просмотров: 722;
