Упругое столкновение
· Абсолютноупругим называют столкновение тел, которое не сопровождается изменением их внутреннего состояния. В ходе абсолютно упругого столкновения происходят превращения механической кинетической энергии движущихся тел в потенциальную энергию и наоборот. При упругом ударе тела деформируются (сплющиваются), их кинетическая энергия частично переходит в потенциальную энергию упругих деформаций. Под действием возникших сил упругости тела стремятся перейти в недеформированное состояние. При этом энергия деформации вновь переходит в энергию поступательного движения, и тела разлетаются в разные стороны.
Таким образом, при анализе процесса упругого столкновения достаточно рассмотреть механическую энергию сталкивающихся тел.
· Центральныйудар – удар, при котором тела до удара движутся вдоль линии, соединяющей их центры масс.
Рассмотрим абсолютно упругий центральный удар двух шаров, имеющих массы m1 и m2 и движущихся поступательно (без вращения) со скоростями V10 и V20. Обозначим через V1 и V2 скорости первого и второго шаров после столкновения. Как отмечено выше, в процессе столкновения выполняется закон сохранения механической энергии:
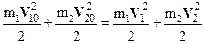 .
.
Если промежуток времени до удара и после него стремится к нулю, то применим также закон сохранения импульса системы:
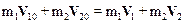 .
.
Соотношения (615) и (6.16) удовлетворяются одновременно, и образуют систему уравнений:
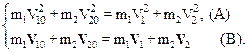
Решая систему (6.17) найдем скорости, которые приобретают шары в результате столкновения. Заметим, что очевидным тривиальным решением системы является решение вида:
V10=V1 и V20=V2.
Физически такое решение означает, что скорости шаров не изменились, а, значит, их столкновение не произошло. Будем считать, что V10¹V1 и V20¹V2. Это замечание позволяет преобразовать уравнения системы следующим образом:
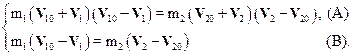
Разделив почленно уравнения системы, имеем:
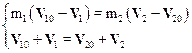
Если умножить второе уравнение системы (6.19) на m2 и вычесть его из первого, то после преобразований получим для скорости V1 первого шара:
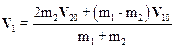 .
.
Умножив второе уравнение системы (6.19) на m1 и сложив со вторым, получим:
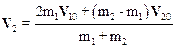
Дата добавления: 2015-08-08; просмотров: 1498;
