Закон сохранения импульса. Уравнение (2.26) показывает, что изменение импульса материальной точки (тела) – dP равно импульсу действия равнодействующей

Уравнение (2.26) показывает, что изменение импульса материальной точки (тела) – dP равно импульсу действия равнодействующей, т. е. dP=Rdt. Если импульс действия силы равен нулю, то из названного выше уравнения следует, что dP равно нулю, и Р – постоянная величина.

· Свободной называют материальную точку (тело), если на нее не действуют силы.

Из сказанного выше следует закон сохранения импульса материальной точки (тела):

· импульс свободной материальной точки остается постоянным.

· Замкнутойсистемойназывается механическая система, на которую не действуют внешние тела (внешние силы отсутствуют).

Из уравнения (2.26) следует, что если импульс действия внешних сил R^ВНЕШdt равен нулю, то приращение импульса dP равно нулю, т. е. Р – постоянная величина.

· Импульс замкнутой механической системы сохраняется.

Причины, вследствие которых импульс действияR^ВНЕШdt=0 равнодействующей равен нулю, а значит, импульс Р системы сохраняется, могут быть разными.

1. R=0, потому что внешние силы (все F_i º0) вообще не действуют на систему.

2. Rdt=0, потому что сумма внешних сил 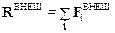равна нулю.

Механическаясистеманазывается скомпенсированной, если действующие на нее внешние силы уравновешены (скомпенсированы), т. е.

.

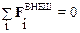· Импульс скомпенсированной механической системы сохраняется.

Пункты 1 и 2 позволяют дать общую формулировку законасохранения импульса системы:

· Импульсзамкнутой (скомпенсированной) механическойсистемыостается постояннымприлюбыхизменениях, произошедшихвней.

Уравнение закона сохранения импульса записывают так:

,

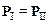здесь 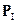и и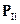мпульс системы, соответственно, в первом и втором состоянии.

Два следующих случая, наиболее часто встречающихся в задачах, требуют особо внимательного рассмотрения.

1. Если время взаимодействия мало dt®0, то можно считать, что Rdt=0 (строго говоря, Rdt®0). Этим условием можно пользоваться, если равнодействующая внешних сил является величиной ограниченной. Например, в задаче о движении осколков снаряда после его разрыва, на них действует сила тяжести mg, поэтому суммарный импульс образовавшейся системы будет изменяться на величину mgt (m - масса снаряда, t – время, прошедшее разрыва). Если рассматривать очень малый промежуток времени dt, то величинаmgdt оказывается много меньше начального импульса снаряда и его изменением можно пренебречь. С формальной точки зрения рассматривают два различных состояния системы, отстоящих друг от друга на бесконечно малый промежуток времени.

Так как импульс является векторной величиной, то уравнению (6.1) соответствует система трех скалярных уравнений для проекций:

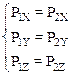
В силу (2.22) и (2.26) для изменения проекций импульса на оси координат справедливы соотношения:

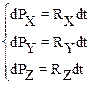
2. Часто приходится рассматривать незамкнутые системы, когда в направлении i-ой оси координат проекция равнодействующей R_i=0. В этом случае сохраняется только проекция импульса на i-ю ось. Например: при условии, что 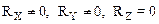имеем:

.

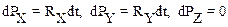Последнее соотношение выражает законсохранения проекции импульса и означает, что

P_2Z=P_1Z.