Кинетическая энергияпоступательного движения

Пусть на материальную точку, масса которой равна m, действует сила F. Запишем уравнение движения этой точки:

.

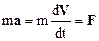Умножим обе части уравнения скалярно на элементарное перемещение dr и преобразуем полученное выражение с учетом того, что элементарное перемещение dr=Vdt:

Таким образом, получаем

.

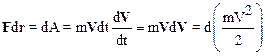Проинтегрируем обе части полученного равенства:

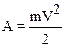
· Кинетическойэнергиейпоступательного движения материальной точки (тела) называют скалярную величину Т= , равную одной второй произведения ее (его) массы на квадрат скорости.

Соотношение (5.13) позволяет указать физический смысл кинетической энергии. Кинетическая энергия показывает, какую работу совершили силы, чтобы покоящемуся первоначально телу сообщить скорость V.

Формула для кинетической энергии была получена с использованием второго закона Ньютона, поэтому она верна только в инерциальной системе отсчета. Заметим, что величина кинетической энергии материальной точки зависит от выбора системы отсчета, поскольку ее скорость в разных ИСО различна (см. (2.4.)). Можно показать, что кинетическая энергия Т в некоторой системе отсчета К равна:

,

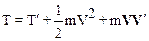где m – масса частицы (тела), T ¢ – кинетическая энергия материальной точки в подвижной системе отсчета К¢, движущейся со скоростью V относительно неподвижной системы К, 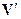– скорость частицы (центра масс тела) относительно подвижной системы отсчета К¢.

Кинетическая энергия – величина аддитивная, т. е.

· кинетическаяэнергиямеханическойсистемы равна сумме кинетических энергий всех ее составляющих:

,

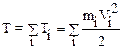здесь m_i и V_i – масса и скорость частиц (тел) системы.