Закон всемирного тяготения Ньютона
Две материальные точки с массами 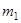 и
и 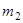 , находящиеся на расстоянии
, находящиеся на расстоянии 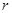 друг от друга притягиваются друг к другу с силой
друг от друга притягиваются друг к другу с силой
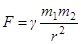 ,
,
где 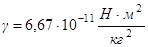 - гравитационная постоянная.
- гравитационная постоянная.

В общем случае двух тел произвольной формы можно мысленно разбить их на малые элемен-ты и просуммировать силы взаимодействия между ними:
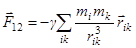 .
.
Таким образом можно, например, показать, что сила гравитационного взаимодействия между двумя однородными шарами с массами 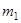 ,
, 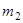 и расстоянием между центрами
и расстоянием между центрами 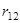 равна
равна
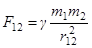 .
.
Из закона всемирного тяготения следует, что любая материальная точка создает вокруг себя силовое (гравитационное) поле, действующее на другие материальные точки. Оно относится к классу так называемых центральных полей, для которых сила может быть представлена в виде:
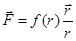 ,
,
где 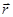 - радиус-вектор, проведенный из точки, называемой центром силового поля, в данную точку.
- радиус-вектор, проведенный из точки, называемой центром силового поля, в данную точку.
Рассмотрим одно важное свойство движения в центральном поле. Для момента количества движения материальной точки в этом случае имеем:
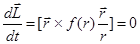 , или
, или 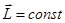 .
.
Таким образом, при движении материальной точки в гравитационном поле, создаваемом другой материальной точкой, сохраняется момент количества движения 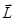 .
.
Отсюда следует, что траектория движения материальной точки в центральном поле целиком лежит в плоскости перпендикулярной вектору 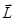 (плоская кривая, рис. 3). Такими кривыми являются траектории движения планет вокруг Солнца и траектории искус-ственных спутников Земли.
(плоская кривая, рис. 3). Такими кривыми являются траектории движения планет вокруг Солнца и траектории искус-ственных спутников Земли.

Потенциальная энергия частицы в гравитационном поле.
Проекция силы потенциального поля на направление 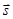 связана с потенциальной энергией соотношением (лекция 5)
связана с потенциальной энергией соотношением (лекция 5)
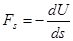 .
.
Выберем в качестве 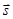 направление радиуса-вектора
направление радиуса-вектора 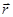 от материальной точки
от материальной точки 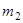 к мате-риальной точке
к мате-риальной точке 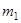 . Тогда
. Тогда
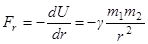 .
.
Отсюда, полагая 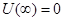 , получим
, получим
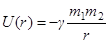 .
.
На основании анализа наблюдений положения планет, проведенных Тихо Браге, Кеплер сформулировал законы их движения.
Законы Кеплера.
1. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.
2. Радиус-вектор планеты в равные времена описывает равные площади.
3. Квадраты времен обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг Солнца.
Законы Кеплера можно получить с помощью 2-го закона Ньютона и закона всемирного тяготения.
1-ый закон Кеплера.
 Так как траектория планеты является плоской, сначала введем в этой плоскости декартову систему координат
Так как траектория планеты является плоской, сначала введем в этой плоскости декартову систему координат  с началом в Солнце. Однако, оказалось, что уравнения движения планеты удается проинтегрировать до конца лишь в так называемых полярных координатах
с началом в Солнце. Однако, оказалось, что уравнения движения планеты удается проинтегрировать до конца лишь в так называемых полярных координатах  , связанных с декартовыми соотношениями (рис. 3)
, связанных с декартовыми соотношениями (рис. 3)
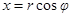 ,
, 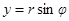 .
.
При движении планеты вокруг Солнца сохраняются ее полная энергия и проекция момента количества движения на ось 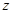 . В полярных координатах эти законы сохранения имеют вид:
. В полярных координатах эти законы сохранения имеют вид:
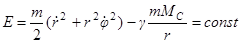 ,
,
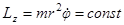 .
.
Здесь точками обозначены производные по времени, 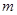 - масса планеты,
- масса планеты, 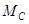 - масса Солнца. Интегрируя эти уравнения можно показать, что при
- масса Солнца. Интегрируя эти уравнения можно показать, что при 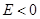 траектория является эллипсом, то есть выполняется 1-ый закон Кеплера. При
траектория является эллипсом, то есть выполняется 1-ый закон Кеплера. При 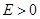 траектория представляет собой гиперболу, а при
траектория представляет собой гиперболу, а при 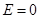 - параболу.
- параболу.
Вообще существует два вида движения в гравитационном поле. При инфинитном движении материальная точка может удалиться сколь угодно далеко от ее начального положения. В случае финитного движения траектория не может выйти за пределы некоторой ограни-ченной области пространства. При 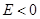 траектория всегда будет финитной, так как при
траектория всегда будет финитной, так как при 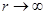 полная энергия
полная энергия 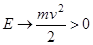 , что противоречит исходному предположению. При
, что противоречит исходному предположению. При 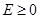 является инфинитной.
является инфинитной.
2 – ой закон Кеплера.
Этот закон является следствием сохранения момента импульса, так как площадь описы-ваемая радиусом-вектором планеты в единицу времени
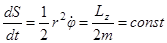 .
.
3 – ий закон Кеплера.
Его легко получить для частного случая движения по окружности:
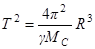 .
.
Космические скорости.
1-ая космическая скорость – скорость тела, движущегося вблизи поверхности Земли по финитной траектории:
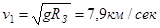 .
.
2-ая космичская скорость – скорость тела вблизи поверхности Земли, движущегося под действием ее поля тяготения по инфинитной траектории:
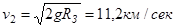 .
.
3 – я космическая скорость – скорость тела вблизи поверхности Земли, движущегося по траектории инфинитной по отношению к Солнцу. В зависимости от положения Земли она варьируется в интервале примерно от 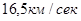 до
до 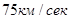 .
.
Дата добавления: 2015-08-08; просмотров: 948;
