Упругие свойства жидкостей и газов.

Газы и жидкости обладают объемной упругостью но не оказывают сопротивления дефор-мации сдвига. В состоянии равновесия напряжение в жидкости или газе (его в этом случае принято называть давлением) всегда нормально к площадке, на которую оно действует. Давление определяется как предел отношения (см. рис. 1)

.

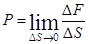Здесь 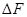- сила, действующая со стороны окружающей жидкости на малую площадку 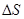. Давление является скалярной величиной, так как оно не зависит от ориентации этой площадки.

Жидкости малосжимаемы. Поэтому для описания многих явле-ний часто используется модель абсолютно несжимаемой жидкости. При движении жидкости в ней могут возникать силы вязкого трения. Идеальная жидкость – при любых движениях силами вязкости можно пренебречь.

Законы гидростатики.

1. Закон Паскаля.

Если нет внешних объемных сил, то в равновесии давление жидкости постоянно во всем объеме.

2. Давление жидкости, находящейся в равновесии в поле тяжести.

Из условия равновесия мысленно выделенного вертикального цилиндра внутри жидкости с плотностью 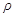легко получить

.

3. Закон Архимеда.

На тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости (сила Архимеда).

Сила Архимеда приложена к центру масс вытесненного объема (точка на рис. 3), называемого центром плавучести тела. Она возникает из-за того, что сила давления со стороны жидкости возрастает с глубиной. Взаимное расположение центра плавучести и центра масс определяют условия равновесия плавающих тел. Если центр масс при полном погружении тела в жидкость расположен ниже центра плавучести, то равновесие устойчиво. В этом случае при небольшом наклоне тела суммарный момент сил возвращает его в исходное положение. В противном случае суммарный момент приводит к увеличению угла наклона. Несколько сложнее обстоит дело при частичном погружении, что как раз чаще всего имеет место на практике. При

наклоне тела в этом случае изменяется форма вытесненного объема и положение центра плавучести (рис. 4). Если точка пересечения направления силы Архимеда и оси симметрии тела (точка 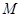на рис. 4) лежит выше центра масс, равновесие устойчиво, если ниже – неустойчиво. При этом центр масс может располагаться выше центра плавучести.

Рассмотрим общие условия равновесия при наличии объемных сил. Пусть на элемент жидкости с объемом действует внешняя сила . Величина называется плотностью объемных сил. Например, для жидкости с плотностью 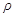, находящейся в поле тяжести, . Выделим элемент жидкости в виде малого цилиндра, ось которого направлена вдоль оси 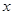, с площадью основания и высотой 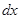. Тогда проекция на ось 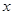сил давления , дейст-вующих на цилиндр равна

.

Аналогичные выражения можно получить для проекций сил давления на ос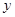и и 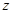. Следовательно, полная сила разности давлений, действующая на элемент , может представлена в виде

, .

В состоянии равновесия 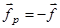( - внешняя объемная сила). Отсюда получаем

.

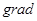
Это уравнение называется основным уравнением гидростатики.

Пример. Равновесие жидкости во вращающемся сосуде.

Будем считать, что жидкость вращается вместе с сосудом. На элемент жидкости с объемом действуют сила тяжести и центробежная сила . Тогда полная объем-ная сила

.

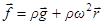Из уравнения гидростатики получаем

, , .

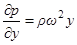При , отсюда получаем уравнение поверхности вращающейся жидкости (параболоид вращения).