Движение по окружности.
1.Равномерное движение по окружности
2.Угловая скорость вращательного движения.
3.Период вращения.
4.Частота вращения.
5.Связь линейной скорости с угловой.
6.Центростремительное ускорение.
7.Равнопеременное движение по окружности.
8.Угловое ускорение в равнопеременном движении по окружности.
9.Тангенциальное ускорение.
10.Закон равноускоренного движения по окружности.
11. Средняя угловая скорость в равноускоренном движении по окружности.
12.Формулы, устанавливающие связь между угловой скоростью, угловым ускорением и углом поворота в равноускоренном движении по окружности.
 1.Равномерное движение по окружности – движение, при котором материальная точка за равные интервалы времени проходит равные отрезки дуги окружности, т.е. точка движется по окружности с постоянной по модулю скоростью. В этом случае скорость равна отношению дуги окружности, пройденной точкой ко времени движения, т.е.
1.Равномерное движение по окружности – движение, при котором материальная точка за равные интервалы времени проходит равные отрезки дуги окружности, т.е. точка движется по окружности с постоянной по модулю скоростью. В этом случае скорость равна отношению дуги окружности, пройденной точкой ко времени движения, т.е.
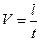
и называется линейной скоростью движения по окружности.
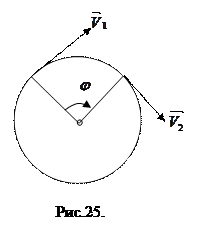
Как и в криволинейном движении вектор скорости направлен по касательной к окружности в направлении движения (Рис.25).
2. Угловая скорость в равномерном движении по окружности – отношение угла поворота радиуса ко времени поворота:
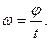
В равномерном движении по окружности угловая скорость постоянна. В системе СИ угловая скорость измеряется в(рад/c). Один радиан – рад это центральный угол, стягивающий дугу окружности длиной равной радиусу. Полный угол содержит 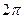 радиан, т.е. за один оборот радиус поворачивается на угол
радиан, т.е. за один оборот радиус поворачивается на угол 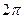 радиан.
радиан.
3. Период вращения – интервал времени Т, в течении которого материальная точка совершает один полный оборот. В системе СИ период измеряется в секундах.
4. Частота вращения – число оборотов 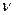 , совершаемых за одну секунду. В системе СИ частота измеряется в герцах ( 1Гц = 1
, совершаемых за одну секунду. В системе СИ частота измеряется в герцах ( 1Гц = 1 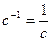 ) . Один герц – частота, при которой за одну секунду совершается один оборот. Легко сообразить, что
) . Один герц – частота, при которой за одну секунду совершается один оборот. Легко сообразить, что 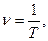
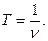
Если за время t точка совершает n оборотов по окружности то 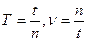 .
.
Зная период и частоту вращения, угловую скорость можно вычислять по формуле:
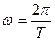 или
или 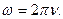
5 Связь линейной скорости с угловой. Длина дуги окружности равна 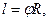 где
где 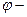 центральный угол, выраженный в радианах, стягивающий дугу
центральный угол, выраженный в радианах, стягивающий дугу 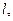
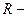 радиус окружности. Теперь линейную скорость запишем в виде
радиус окружности. Теперь линейную скорость запишем в виде
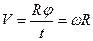 , где
, где 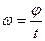 .
.
 Часто бывает удобно использовать формулы:
Часто бывает удобно использовать формулы: 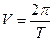 или
или 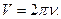 Угловую скорость часто называют циклической частотой, а частоту
Угловую скорость часто называют циклической частотой, а частоту 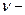 линейной частотой.
линейной частотой.
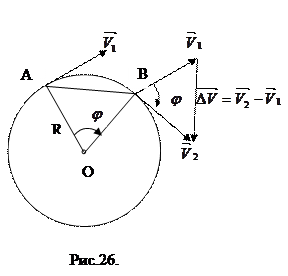
6. Центростремительное ускорение. В равномерном движении по окружности модуль скорости остаётся неизменным 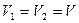 , а направление её непрерывно меняется (Рис.26). Это значит, что тело, движущееся равномерно по окружности, испытывает ускорение, которое направлено к центру и называется центростремительным ускорением.
, а направление её непрерывно меняется (Рис.26). Это значит, что тело, движущееся равномерно по окружности, испытывает ускорение, которое направлено к центру и называется центростремительным ускорением.
Пусть за промежуток времени 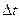 прошло путь равный дуге окружности
прошло путь равный дуге окружности 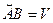
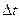 . Перенесём вектор
. Перенесём вектор 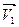 , оставляя его параллельным самому себе, так чтобы его начало совпало с началом вектора
, оставляя его параллельным самому себе, так чтобы его начало совпало с началом вектора 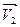 в точке В. Модуль изменения скорости равен
в точке В. Модуль изменения скорости равен 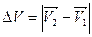 , а модуль центростремительного ускорения равен
, а модуль центростремительного ускорения равен 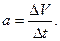
На Рис.26 треугольники АОВ и ДВС равнобедренные и углы при вершинах О и В равны, как углы с взаимно перпендикулярными сторонами АО 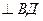 и ОВ
и ОВ 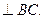 Это значит, что треугольники АОВ и ДВС подобные. Следовательно
Это значит, что треугольники АОВ и ДВС подобные. Следовательно 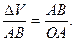 Если
Если 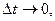 то есть интервал времени
то есть интервал времени 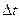 принимает сколь угодно малые значения, то дугу
принимает сколь угодно малые значения, то дугу 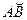 можно приближенно считать равной хорде АВ, т.е.
можно приближенно считать равной хорде АВ, т.е. 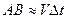 . Поэтому можем записать
. Поэтому можем записать 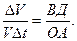 Учитывая, что ВД=
Учитывая, что ВД= 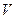 , ОА=R получим
, ОА=R получим 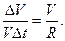 Умножая обе части последнего равенства на
Умножая обе части последнего равенства на 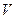 , получим
, получим 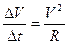 и далее выражение для модуля центростремительного ускорения в равномерном движении по окружности:
и далее выражение для модуля центростремительного ускорения в равномерном движении по окружности: 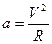 .
.  Учитывая, что
Учитывая, что 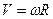 получим две часто применяемые формулы:
получим две часто применяемые формулы:
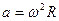 ,
, 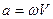 .
.
Итак, в равномерном движении по окружности центростремительное ускорение постоянно по модулю.
Легко сообразить, что в пределе при 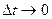 , угол
, угол 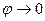 . Это значит, что углы при основании ДС треугольника ДВС стремятся значению
. Это значит, что углы при основании ДС треугольника ДВС стремятся значению 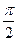 , а вектор изменения скорости
, а вектор изменения скорости 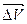 становится перпендикулярным к вектору скорости
становится перпендикулярным к вектору скорости 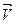 , т.е. направлен по радиусу к центру окружности.
, т.е. направлен по радиусу к центру окружности.
7. Равнопеременное движение по окружности – движение по окружности, при котором за равные интервалы времени угловая скорость изменяется на одну и ту же величину.
8. Угловое ускорение в равнопеременном движении по окружности – отношение изменения угловой скорости к интервалу времени 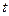 , в течении которого это изменение произошло, т.е.
, в течении которого это изменение произошло, т.е.
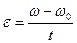 ,
,
где 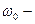 начальное значение угловой скорости,
начальное значение угловой скорости, 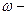 конечное значение угловой скорости,
конечное значение угловой скорости, 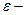 угловое ускорение, в системе СИ измеряется в
угловое ускорение, в системе СИ измеряется в 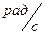 . Из последнего равенства получим формулы для вычисления угловой скорости
. Из последнего равенства получим формулы для вычисления угловой скорости
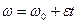 и
и 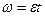 , если
, если 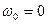 .
.
Умножая обе части этих равенств на 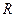 и учитывая, что
и учитывая, что 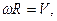
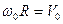 ,
, 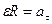 - тангенциальное ускорение, т.е. ускорение, направленное по касательной к окружности , получим формулы для вычисления линейной скорости:
- тангенциальное ускорение, т.е. ускорение, направленное по касательной к окружности , получим формулы для вычисления линейной скорости:
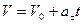 и
и 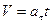 , если
, если 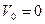 .
.
9. Тангенциальное ускорение численно равно изменению скорости в единицу времени и направлено вдоль касательной к окружности. Если 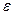 >0,
>0, 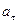 >0, то движение равноускоренное. Если
>0, то движение равноускоренное. Если 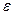 <0 и
<0 и 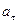 <0 – движение.
<0 – движение.
10. Закон равноускоренного движения по окружности. Путь, пройденный по окружности за время 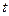 в равноускоренном движении, вычисляется по формуле:
в равноускоренном движении, вычисляется по формуле:
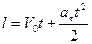 .
.
Подставляя сюда 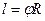 ,
,  ,
,  сокращая на
сокращая на 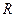 , получим закон равноускоренного движения по окружности:
, получим закон равноускоренного движения по окружности:
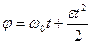 , или
, или 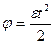 , если
, если 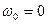 .
.
Если же движение равнозамедленное, т.е. 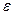 <0, то
<0, то
 .
.
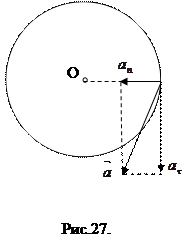 11.Полное ускорение в равноускоренном движении по окружности. В равноускоренном движении по окружности центростремительное ускорение с течением времени возрастает, т.к. благодаря тангенциальному ускорению возрастает линейная скорость. Очень часто центростремительное ускорение называют нормальным и обозначают как
11.Полное ускорение в равноускоренном движении по окружности. В равноускоренном движении по окружности центростремительное ускорение с течением времени возрастает, т.к. благодаря тангенциальному ускорению возрастает линейная скорость. Очень часто центростремительное ускорение называют нормальным и обозначают как  . Так как
. Так как 
 полное ускорение в данный момент определяют по теореме Пифагора
полное ускорение в данный момент определяют по теореме Пифагора 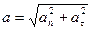 (Рис.27).
(Рис.27).
12. Средняя угловая скорость в равноускоренном движении по окружности. Средняя линейная скорость в равноускоренном движении по окружности равна 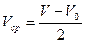 . Подставляя сюда
. Подставляя сюда 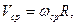
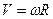 и
и  и сокращая на
и сокращая на 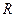 получим
получим
 .
.
Если 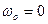 , то
, то 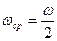 .
.
12. Формулы, устанавливающие связь между угловой скоростью, угловым ускорением и углом поворота в равноускоренном движении по окружности.
Подставляя в формулу 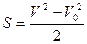 величины
величины  ,
, 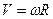 ,
,  ,
, 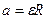 ,
,
и сокращая на 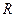 , получим
, получим
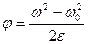 .
.
Если 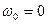 , то
, то  и далее
и далее 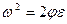 ,
, 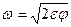 .
.
Лекция- 4. Динамика. 
1. Динамика
2. Взаимодействие тел.
3. Инерция. Принцип инерции.
4. Первый закон Ньютона.
5. Свободная материальная точка.
6. Инерциальная система отсчета.
7. Неинерциальная система отсчета.
8. Принцип относительности Галилея.
9. Преобразования Галилея.
10. Сила.
11. Сложение сил.
12. Масса.
13. Плотность веществ.
14. Центр масс.
15. Второй закон Ньютона.
16. Единица измерения силы.
17. Третий закон Ньютона
1. Динамика есть раздел механики, изучающий механическое движение, в зависимости от сил, вызывающих изменение этого движения.
2.Взаимодействия тел. Тела могут взаимодествовать, как при непосредственном соприкосновенном соприкосновении, так и на расстоянии посредством особого вида материи, называемого физическим полем.
Например, все тела притягиваются друг к другу и это притяжение осуществляется посредством гравитационного поля, а силы притяжения называются гравитационными.
Тела, несущие в себе электрический заряд, взаимодействуют посредством электрического поля. Электрические токи взаимодействуют посредством магнитного поля. Эти силы называют электромагнитными.
Элементарные частицы взаимодействуют посредсвом ядерных полей и эти силы называют ядерными.
3.Инерция. В IV в. до н. э. греческий философ Аристотель утверждал, что причиной движения тела является сила, действующая со стороны другого тела или тел. При этом, по движения мнению Аристотеля постоянная сила сообщает телу постоянную скорость и с прекращением действия силы прекращается движение.
В 16 в. итальянский физик Галилео Галилей, проводя опыты с телами, скатывающимися по наклонной плоскости и с падающими телами показал, что постоянная сила ( в данном случае вес тела) сообщает телу ускорение.
Итак, на основе экспериментов Галилей показал, что сила причина ускорения тел. Приведем рассуждения Галилея. Пусть очень гладкий шар катится по гладкой горизонтальной плоскости. Если шару ничего не мешает, то он может катиться сколь угодно долго. Если же на пути шара насыпать тонкий слой песка, то он очень скоро остановится, т.к. на него подействовала сила трения песка.
Так Галилей пришел к формулировке принципа инерции, согласно которому материальное тело сохраняет состояние покоя или равномерного прямолинейного движения, если на не действуют внешние силы. Часто это свойство материи называют инерцией, а движение тела без внешних воздействий- движением по инерции.
4. Первый закон Ньютона. В 1687 году на основе принципа инерции Галилея Ньютон сформулировал первый закон динамики – первый закон Ньютона:
Материальная точка (тело) находится в состоянии покоя или равномерного прямолинейного движения, если на неё не действуют другие тела, либо силы, действующие со стороны других тел, уравновешены, т.е. скомпенсированы.
5.Свободная материальная точка – материальная точка, на которую не действуют другие тела. Иногда говорят – изолированная материальная точка.
6. Инерциальная система отсчета (ИСО) – система отсчёта, относительно которой изолированная материальная точка движется прямолинейно и равномерно, либо находится в состоянии покоя.
Любая система отсчёта, которая движется равномерно и прямолинейно относительно ИСО является инерциальной,
Приведём ещё одну формулировку первого закона Ньютона: Существуют системы отсчёта, относительно которых свободная материальная точка движется прямолинейно и равномерно, либо находится в состоянии покоя. Такие системы отсчёта называются инерциальными. Часто первый закон Ньютона называют законом инерции.
Первому закону Ньютона можно дать ещё и такую формулировку: всякое материальное тело сопротивляется изменению его скорости. Это свойство материи называется инертностью.
С проявлением этого закона мы сталкиваемся ежедневно в городском транспорте. Когда автобус резко набирает скорость, нас прижимает к спинке сидения. Когда же автобус тормозит, то наше тело заносит по ходу движения автобуса.
7. Неинерциальная система отсчёта –система отсчёта, которая движется неравномерно относительно ИСО.
Тело, которое относительно ИСО находится в состоянии покоя или равномерного прямолинейного движения. Относительно неинерциальной системы отсчёта движется неравномерно.
Любая вращающаяся система отсчёта есть неинерциальная система отсчёта, т.к. в этой системе тело испытывает центростремительное ускорение.
В природе и технике нет тел, которые могли бы служить в качестве ИСО. Например, Земля вращается вокруг своей оси и любое тело на её поверхности испытывает центростремительное ускорение. Однако в течение достаточно коротких промежутков времени систему отсчёта, связанную с поверхностью Земли в некотором приближении можно считать ИСО.
8.Принцип относительности Галилея.ИСО может быть соль угодно много. Поэтому возникает вопрос: как выглядят одни и те же механические явления в разных ИСО? Можно ли используя механические явления, обнаружить движение ИСО, в которой они наблюдаются.
Ответ на эти вопросы дает принцип относительности классической механики, открытый Галилеем.
Смысл принципа относительности классической механики заключается в утверждении: все механические явления протекают совершенно одинаково во всех инерциальных системах отсчёта.
Этот принцип можно сформулировать и так: все законы классической механики выражаются одинаковыми математическими формулами. Иными словами никакие механические опыты не помогут нам обнаружить движение ИСО. Это значит, что попытка обнаружить движение ИСО лишена смысла.
С проявлением принципа относительности мы сталкивались, путишествуя в поездах. В момент, когда наш поезд стоит на станции, а поезд, стоявший на соседнем пути , медленно начинает движение, то в первые мгновения нам кажется, движется наш поезд. Но бывает и наоборот, когда наш поезд плавно набирает ход, нам кажется, что движение начал соседний поезд.
В приведённом примере принцип относительности проявляется в течение малых интервалов времени. С увеличением скорости мы начинаем ощущать толчки раскачивание вагона, т. е. наша система отсчёта становится неинерциальной.
Итак, попытка обнаружить движение ИСО лишена смысла. Следовательно, абсолютно безразлично, какую ИСО считать неподвижной, а какую – движущейся.
9. Преобразования Галилея. Пусть две ИСО 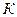 и
и 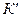 движутся друг относительно друга со скоростью
движутся друг относительно друга со скоростью 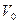 . Согласно с принципом относительности мы можем положить, что ИСО К неподвижна, а ИСО
. Согласно с принципом относительности мы можем положить, что ИСО К неподвижна, а ИСО 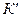 движется относительно
движется относительно 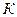 со скоростью
со скоростью 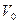 . Для простоты положим, что соответствующие оси координат систем
. Для простоты положим, что соответствующие оси координат систем 
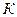 и
и 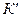 параллельны, а оси
параллельны, а оси  и
и 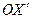 совпадают. Пусть в момент
совпадают. Пусть в момент  начала систем совпадают и движение происходит вдоль осей
начала систем совпадают и движение происходит вдоль осей  и
и 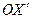 , т.е.
, т.е. 
 (Рис.28)
(Рис.28)
 За время
За время  система
система  прошла путь
прошла путь 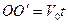 вдоль оси
вдоль оси  . Из Рис.28 получим соотношения между координатами точки m в системах
. Из Рис.28 получим соотношения между координатами точки m в системах 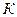 и
и 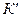

Эти соотношения и называются преобразованиями Галилея. Преобразования Галилея представляют собой математическое выражение принципа относительности Галилея.
 10.Сила – количественная мера взаимодействия тел, в результате которого тела получают ускорения. Сила величина и её направление всегда совпадает с направлением ускорения , которое она сообщает телу,
10.Сила – количественная мера взаимодействия тел, в результате которого тела получают ускорения. Сила величина и её направление всегда совпадает с направлением ускорения , которое она сообщает телу, 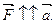
11. Сложение сил. Если частице приложены две силы, то результирующая сила равна их векторной  , т.е. диагонали параллелограмма, построенного на векторах
, т.е. диагонали параллелограмма, построенного на векторах 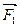 и
и 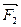 ( Рис.29).
( Рис.29).
Этим же правилом при разложении данной силы на две составляющие силы. Для этого на векторе данной силы, как на диагонали строят параллелограмм, стороны которого совпадают с направлением составляющих сил, приложенных к данной частице.
Если же к частице приложены несколько сил, то результирующая равна геометрической сумме всех сил:
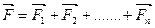 .
.
12.Масса. Опыт показал, что отношение модуля силы к модулю ускорения, которое эта сила сообщает телу, есть величина постоянная для данного тела и называется массой тела:
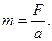
Из последнего равенства следует, что чем больше масса тела, большую силу необходимо приложить, чтобы изменить его скорость. Следовательно, чем больше масса тела тем оно более инертно, т.е. масса есть мера инертности тел. Массу определённую таким образом называют инертной массой.
В системе СИ масса измеряется в килограммах (кг). Один килограмм – это масса дисциллирванной воды в объёме одного кубического дециметра взятой при температуре 
13. Плотность вещества – масса вещества, содержащегося в единице объёма или отношение массы тела к его объёму

Плотность измеряется в (  ) в системе СИ. Зная плотность тела и его объём можно вычислить его массу по формуле
) в системе СИ. Зная плотность тела и его объём можно вычислить его массу по формуле 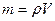 . Зная плотность и массу тела, его объём вычисляют по формуле
. Зная плотность и массу тела, его объём вычисляют по формуле  .
.
14.Центр масс – точка тела, обладающая тем свойством, что, если направление действия силы проходит через эту точку тело движется поступательно. Если же направление действия не проходит через центр масс, то тело перемещается, одновременно вращаясь вокруг своего центра масс
15. Второй закон Ньютона. В ИСО сумма сил, действующих на тело равна произведению массы тела на ускорение, сообщаемое ему этой силой
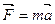 ,
, 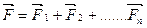 .
.
16.Единица измерения силы. В системе СИ сила измеряется в ньютонах. Один ньютон (н) – это сила, которая действуя на тело массой один килограмм сообщает ему ускорение 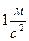 . Поэтому
. Поэтому  .
.
17. Третий закон Ньютона. Силы, с которыми два тела действуют друг на друга, равны по модулю, противоположны по направлению и действуют вдоль одной прямой, соединяющей эти тела:
 ,
,
где 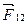 - сила, с которой первое тело действует на второе,
- сила, с которой первое тело действует на второе,  - сила, с которой второе тело действует на первое. Из второго и третьего законов Ньютона следуют равенства:
- сила, с которой второе тело действует на первое. Из второго и третьего законов Ньютона следуют равенства:
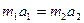 ,
,  .
.
Иными словами модули ускорений, которые при взаимодействии получают два тела, обратно пропорциональны их массам.
Время взаимодействия для этих двух тел одно и то же поэтому модули скоростей, которые они получают в результате взаимодействия обратно пропорциональны их массам:

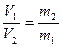 .
.

Дата добавления: 2015-08-08; просмотров: 19667;
