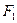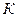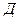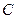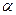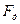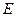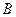Лекция – 7.
1. Динамка поступательного движения.
2. Поступательное движение с учётом трения.
3. Движение по наклонной плоскости.
4. Движение грузов, связанных нитью, перекинутой через блок.
5. Применение законов Ньютона к движению материальной точки по окружности.
6. Движение искусственных спутников. Первая космическая скорость.
1. Динамика поступательного движения тела. Пусть некоторое тело движется поступательно вдоль прямой линии. В этом случае за положительное направление сил принимают направление направлении, совпадающее с направлением ускорения тела. Это значит, что силы или их проекции на данную прямую, направления которых совпадают с направлением ускорения записываются в уравнении движения со знаком (+), а силы направленные против ускорения – со знаком (-). Кроме этого необходимо помнить, что сила трения всегда направлена противоположно вектору скорости
 2. Поступательное движение с учетом трения. Рассмотрим несколько примеров поступательного движения с учетом трения.
2. Поступательное движение с учетом трения. Рассмотрим несколько примеров поступательного движения с учетом трения.
Пусть тело движется прямолинейно и равномерно с некоторой скоростью  по шероховатой горизонтальной плоскости. Это значит, что все силы, действующие на тело скомпенсированы согласно первому закону Ньютона, т.е.
по шероховатой горизонтальной плоскости. Это значит, что все силы, действующие на тело скомпенсированы согласно первому закону Ньютона, т.е. 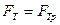 ,
, 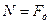 , где
, где 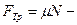 сила трения,
сила трения, 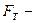 сила тяги,
сила тяги, 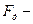 сила, с которой тело прижимается к плоскости, но
сила, с которой тело прижимается к плоскости, но 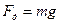 , N –реакция опоры
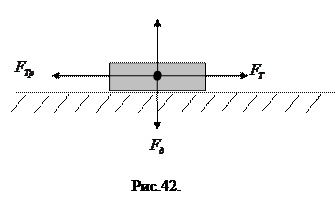
, N –реакция опоры 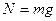 (рис.42).Если это тело, имея скорость
(рис.42).Если это тело, имея скорость 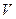 , под действием сил тяги начнёт двигаться ускоренно, то
, под действием сил тяги начнёт двигаться ускоренно, то 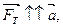
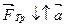 и
и 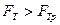 . Тогда по второму закону Ньютона запишем
. Тогда по второму закону Ньютона запишем
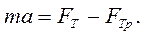
Когда действие силы тяги прекратится 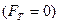 , тело будет двигаться замедленно, следовательно, ускорение, как и сила трения будет направлена против скорости
, тело будет двигаться замедленно, следовательно, ускорение, как и сила трения будет направлена против скорости 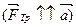 . По второму закону Ньютона запишем
. По второму закону Ньютона запишем
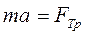 .
.
3.Движение по наклонной плоскости. Пусть тело массы m находится на наклонной плоскости с углом наклона к горизонту 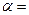 <САБ (Рис.43). Силу тяжести mg разложим по правилу параллелограмма на две составляющие
<САБ (Рис.43). Силу тяжести mg разложим по правилу параллелограмма на две составляющие 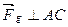 ,
, 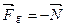 , где
, где  реакция опоры и
реакция опоры и 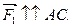 На Рис.43 N=KE, mg=DK.
На Рис.43 N=KE, mg=DK.
|

|
|
|






| |

 Углы
Углы 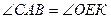 , как углы с взаимно перпендикулярными сторонами
, как углы с взаимно перпендикулярными сторонами 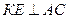 ,
, 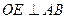 . Треугольник ОКЕ прямоугольный, что следует из построения
. Треугольник ОКЕ прямоугольный, что следует из построения 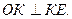 Из Рис.43 следует
Из Рис.43 следует 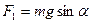 ,
, 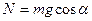 .
.
|
|
|
|
|
|
|
|


 Если тело движется равномерно вверх по наклонной плоскости под действием силы тяги
Если тело движется равномерно вверх по наклонной плоскости под действием силы тяги 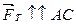 , то силы параллельные АС скомпенсированы согласно первому закону Ньютона. Поэтому
, то силы параллельные АС скомпенсированы согласно первому закону Ньютона. Поэтому 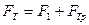 , учитывая далее, что
, учитывая далее, что 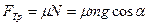 получим
получим
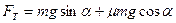 .
.
Если же тело под действием силы тяги движется равномерно вниз по наклонной плоскости, 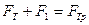 или
или
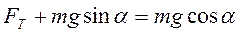 .
.
Если тело под действием силы тяги 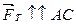 движетсявверх по наклонной плоскости с ускорением а, то по второму закону Ньютона, учитывая, что
движетсявверх по наклонной плоскости с ускорением а, то по второму закону Ньютона, учитывая, что 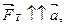
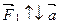 и
и 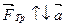 , запишем
, запишем
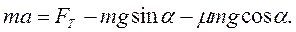
Для движениявниз с ускорением а, учитывая, что 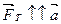 ,
, 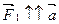 ,
, 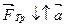 получим
получим
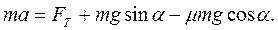
4.Движение грузов, связанных нитью, переброшенной через блок (Рис.44). Для определённости положим 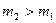 , тогда груз
, тогда груз 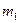 движется вверх с ускорением а, груз
движется вверх с ускорением а, груз 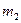 - с тем же ускорением вверх.
- с тем же ускорением вверх.
По второму закону Ньютона уравнения движения грузов 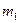 и
и 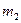 запишем в виде:
запишем в виде:

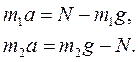
Решая эту систему уравнений, в зависимости от данных можно найти все входящие в них величины.
5. Применение законов Ньютона к движению материальной точки по окружности.В равномерном движении по окружности центростремительное ускорение обусловлено действием на тело центростремительной силы, которая по второму закону Ньютона равна 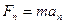 , учитывая, что цнетростремительное ускорение равно
, учитывая, что цнетростремительное ускорение равно 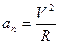 получим выражение центростремительной силы в виде:
получим выражение центростремительной силы в виде:
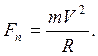
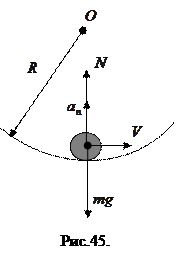 Рассмотрим несколько примеров движения по окружности.
Рассмотрим несколько примеров движения по окружности.
Пусть по вогнутому мосту с радиусом кривизны R движется тело массы m со скоростью 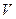 (Рис.45). В нижней части моста на тело действует сила тяжести, направленная вертикально вниз и реакция опоры N – вертикально вверх. Центростремительное ускорение
(Рис.45). В нижней части моста на тело действует сила тяжести, направленная вертикально вниз и реакция опоры N – вертикально вверх. Центростремительное ускорение 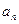 направлено вертикально вверх, т.е. к центру кривизны моста О. По второму закону Ньютона запишем
направлено вертикально вверх, т.е. к центру кривизны моста О. По второму закону Ньютона запишем
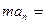
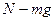 .
.
Отсюда получаем реакцию опоры или вес тела:
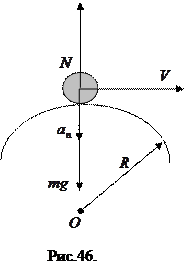

Пусть теперь тело проходит верхнюю точку выпуклого моста (Рис.46). Сила тяжести и центростремительное ускорение направлены вертикально вниз, а реакция опоры пртивонаправлена им. По второму акону Ньютона запишем
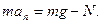
Отсюда получаем вес тела
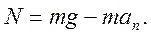
Из последнего равенства следует, что при движении по выпуклому мосту вес тела меньше силы тяжести. Поэтому для уменьшения нагрузки на мосты их делают выпуклыми.
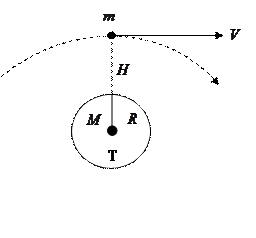
6.Движение искусственных спутников. Первая космическая скорость.Пусть искусственный спутник массы m движется по круговой орбите со скоростью 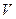 на высоте Н над поверхностью Земли, R – радиус Земли, М – масса Земли (Рис.47).
на высоте Н над поверхностью Земли, R – радиус Земли, М – масса Земли (Рис.47).
Роль центростремительной силы на высоте Н играет сила тяжести, поэтому запишем равенство
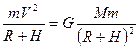 .
.
 Отсюда легко получим скорость искусственного спутника на высоте Н
Отсюда легко получим скорость искусственного спутника на высоте Н
 .
.
Эта формула справедлива для любой планеты. Первой космической скоростью называют скорость спутника, движущегося по круговой орбите на очень малой высоте над поверхностью планеты ( Н <<R). Пренебрегая Н в формуле скорости искусственного спутника, получим выражение первой космической скорости
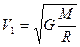 .
.
Учитывая, что 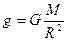 , получим часто употребляемое выражение первой космической скорости
, получим часто употребляемое выражение первой космической скорости
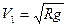 .
.
Первая космическая скорость для искусственного спутника Земли составляет 7.9 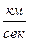 .
.
Дата добавления: 2015-08-08; просмотров: 2006;