Лекция – 2. Кинематика. Часть – 2.
1. Неравномерное прямолинейное движение.
2. Путь, пройденный в неравномерном прямолинейном движении.
3. Ускорение.
4. Равнопеременное движение.
5. Равноускоренное прямолинейное движение.
6. Равнозамедленное прямолинейное движение.
7. Перемещение в равноускоренном прямолинейном движении.
8. Перемещение в равнозамедленном прямолинейном движении.
9. Средняя скорость в равноускоренном движении.
10. Формулы, устанавливающие связь между скоростью, ускорением и пройденным путём в равноускоренном движении.
11. График зависимости координаты (перемещения) от времени в равноускоренном прямолинейном движении.
12. Свободное падение тел.
13. Движение тела, брошенного под углом к горизонту, высота и дальность полёта.
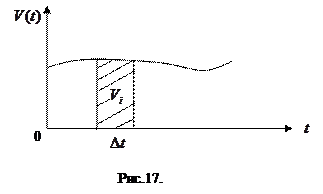
 1.Неравномерное прямолинейное движение – это движение, при котором тело, перемещаясь вдоль прямой линии, за равные промежутки времени проходит разные перемещения, т.е. скорость меняется по величине с течением времени и является функцией времени V (t). График зависимости величины скорости от времени, т. е. график функции V (t) представлен на Рис.17
1.Неравномерное прямолинейное движение – это движение, при котором тело, перемещаясь вдоль прямой линии, за равные промежутки времени проходит разные перемещения, т.е. скорость меняется по величине с течением времени и является функцией времени V (t). График зависимости величины скорости от времени, т. е. график функции V (t) представлен на Рис.17 
 2. Путь, пройденный в неравномерном прямолинейном движении.Разобьём всё время движения на очень малые интервалы
2. Путь, пройденный в неравномерном прямолинейном движении.Разобьём всё время движения на очень малые интервалы 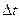 , в течение которых скорость можно считать приближенно постоянной и равной средней скорости
, в течение которых скорость можно считать приближенно постоянной и равной средней скорости 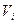 движения в течение времени
движения в течение времени 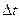 . Тогда путь
. Тогда путь 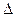
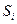 , пройденный за время
, пройденный за время 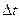 с постоянной скоростью
с постоянной скоростью 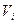 вычислим по формуле:
вычислим по формуле: 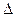
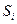 =
= 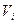
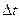 . На Рис.17 этот путь равен площади заштрихованной фигуры, которую ввиду малости
. На Рис.17 этот путь равен площади заштрихованной фигуры, которую ввиду малости 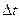 можно считать прямоугольником со сторонами
можно считать прямоугольником со сторонами 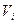 и
и 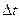 . Складывая отрезки пути
. Складывая отрезки пути 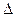
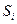 получим площадь фигуры, образованной графиком скорости осью времени.
получим площадь фигуры, образованной графиком скорости осью времени.
 Итак, путь, пройденный телом при неравномерном прямолинейном движении численно равен площади графиком зависимости скорости движения тела от времени.
Итак, путь, пройденный телом при неравномерном прямолинейном движении численно равен площади графиком зависимости скорости движения тела от времени.
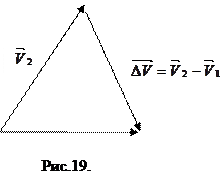
3. Ускорение. При произвольном движении точки модуль и направление скорости непрерывно меняются Рис.18. Совместим начала векторов 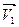 и
и 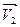 , тогда вектор
, тогда вектор 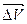 =
= 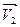 -
- 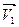 есть изменение скорости точки и пусть
есть изменение скорости точки и пусть 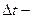 интервал времени,в течение которого это изменение произошло Рис.19.
интервал времени,в течение которого это изменение произошло Рис.19.
Средним ускорением называют отношение изменение скорости к интервалу времени, в течение которого это изменение произошло:
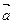 =
= 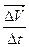 .
. 
В системе СИ ускорение измеряется в ( 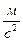 ), ускорение векторная величина.
), ускорение векторная величина.
Мгновенное ускорение – среднее ускорение за бесконечно малый интервал времени:


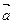 =
= 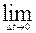
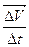 .
.
4. Равнопеременное движение - движение с постоянным по модулю направлению ускорением 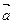 =
= 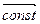 . В этом случае скорость точки за равные интервалы времени изменяется на одну и ту же величину, а ускорение вычисляется по формуле:
. В этом случае скорость точки за равные интервалы времени изменяется на одну и ту же величину, а ускорение вычисляется по формуле:
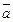 =
= 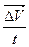
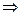
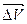 =
= 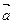 t
t
где 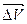 =
= 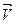
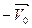 изменение скорости за время t,
изменение скорости за время t, 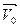 - начальная скорость точки в момент времени t=0,
- начальная скорость точки в момент времени t=0, 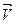 - конечная скорость точки в момент t, т.е.
- конечная скорость точки в момент t, т.е. 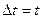 . Теперь можно записать:
. Теперь можно записать: 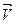
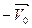 =
= 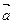 t и далее
t и далее
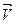 =
= 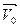 +
+ 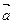 t .
t .
Если ускоренное началось из состояния покоя, т.е. 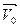 = 0, то
= 0, то 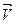 =
= 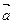 t .
t .
5. Равноускоренное прямолинейное движение – движение, при котором траектория есть прямая линия , ускорение постоянная величина и направлено вдоль прямой причём направления скорости и ускорения совпадают, т.е. 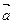
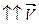 . В этом случае модуль скорости возрастает со временем. Прямолинейность траектории позволяет все вычисления с модулями скорости и ускорения по формулам:
. В этом случае модуль скорости возрастает со временем. Прямолинейность траектории позволяет все вычисления с модулями скорости и ускорения по формулам: 
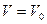 + аt и
+ аt и 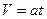 , если
, если 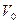 =0.
=0.
Таким образом, в прямолинейном равноускоренном движении модуль скорости возрастает пропорционально времени. График зависимости скорости от времени представлен Рис. 20. 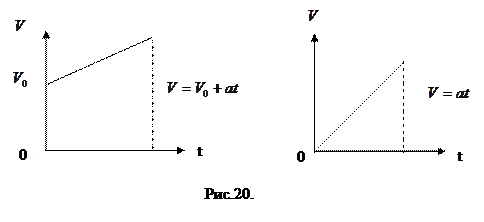
6. Равнозамедленное прямолинейное движение – прямолинейное движение с постоянным по модулю и направлению ускорением, при этом векторы скорости и ускорения противонаправлены, т. е. антипараллельны 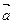
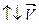 . В этом случае все вычисления также можно проводить с модулями скорости и ускорения, учитывая , что ускорение отрицательно
. В этом случае все вычисления также можно проводить с модулями скорости и ускорения, учитывая , что ускорение отрицательно
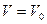
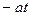 .
.
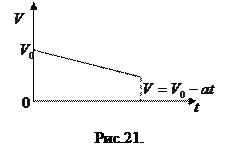 Итак, скорость в прямолинейном равнозамедленном движении линейно убывает с течением времени. Зависимость скорости от времени в равнозамедленном прямолинейном движении представлена графиком на Рис.21.
Итак, скорость в прямолинейном равнозамедленном движении линейно убывает с течением времени. Зависимость скорости от времени в равнозамедленном прямолинейном движении представлена графиком на Рис.21.
7. Перемещение в равноускоренном прямолинейном движении. Уравнение прямолинейного равноускоренного движения. Пусть материальная точка движется по оси  х и пусть в начальный момент времени t=0 она имела начальную скорость
х и пусть в начальный момент времени t=0 она имела начальную скорость 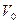 . Перемещение, пройденное точкой за время t численно равно площади под графиком зависимости скорости от времени, т.е. площади трапеции с основаниями
. Перемещение, пройденное точкой за время t численно равно площади под графиком зависимости скорости от времени, т.е. площади трапеции с основаниями 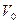 и
и 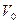 +аt и высотой t Рис.20
+аt и высотой t Рис.20

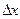 =
= 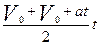

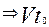 +
+ 
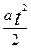 , если
, если 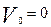 , то
, то 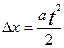 .
.
Учитывая, что 
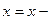
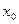 получим закон равноускоренного прямолинейного движения:
получим закон равноускоренного прямолинейного движения:

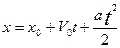 .
.
Совмещая начальное положение тела с началом отсчёта на оси х, т.е. полагая 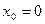 получим:
получим: 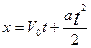 . Если же движение началось из состояния покоя, т.е.
. Если же движение началось из состояния покоя, т.е. 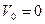 , закон равноускоренного прямолинейного запишем в виде:
, закон равноускоренного прямолинейного запишем в виде: 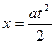 .
.
8. Перемещение в равнозамедленном прямолинейном движении. Для равнозамедленного движения ускорение отрицательно а< 0 и перемещение вычисляется по формуле:
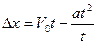 ,
,
а закон движения записывается в виде: 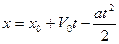 , если
, если 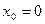 , то
, то 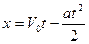 .
.
Если 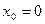 , то координата х численно равна пройденному пути. Поэтому путь, пройденный в равноускоренном движении, вычисляется по формуле:
, то координата х численно равна пройденному пути. Поэтому путь, пройденный в равноускоренном движении, вычисляется по формуле:
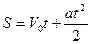 и
и 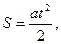 при
при 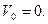
Для равнозамедленного движения а < 0 и 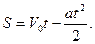
9.Средняя скорость в равноускоренном движении получается делением пройденного пути на время движения
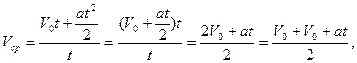
Учитывая, что 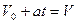 получим
получим 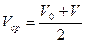 . Таким образом средняя скорость в равноускоренном движении (равнопеременном) равна среднему арифметическому начальной и конечной скоростей. Если
. Таким образом средняя скорость в равноускоренном движении (равнопеременном) равна среднему арифметическому начальной и конечной скоростей. Если 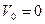 , то
, то 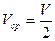 .
.
10. Формулы, устанавливающие связь между ускорением, скоростью и пройденным путём в равноускоренном (равнопеременном) движении. Пусть тело, имея начальную скорость 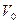 и двигаясь с ускорением а, за время t достигло скорости
и двигаясь с ускорением а, за время t достигло скорости 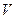 и прошло путь S. Тогда S=
и прошло путь S. Тогда S= 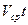 . Подставляя сюда
. Подставляя сюда 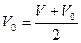 , t=
, t= 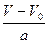 получим
получим
S= 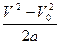 .
.
Если 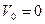 , то
, то 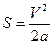 и далее получим
и далее получим 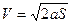 .
.
Дата добавления: 2015-08-08; просмотров: 2144;
