I. Вводная часть

Различают два режима движения жидкости: ламинарный и турбулентный. Термин «ламинарный» произошёл от латинского слова «lamina» - слой, а термин «турбулентный» - от латинского слова «turbulentus» - беспорядочный.

При ламинарном режиме частицы жидкости движутся отдельными не смешивающимися друг с другом параллельными струйками. При турбулентном режиме частицы жидкости движутся беспорядочно, хаотически, отдельные струйки перемешиваются между собой.

На существование в природе двух режимов движения жидкости впервые указал проф. Д. И. Менделеев^*) в 1880 г. в работе «О сопротивлении жидкости и воздухоплавании»

Экспериментальное изучение режимов движения жидкости было выполнено О. Рейнольдсом^**) в 1883г.

Режим движения жидкости зависит от размеров живого сечения потока, вязкости жидкости и скорости её движения: при малых скоростях наблюдается ламинарный режим, а при больших – турбулентный. Скорость, при которой один режим движения переходит в другой, Рейнольдс назвал критической.

Различают две критические скорости – верхнюю критическую скорость V_в.к. – при которой ламинарный режим движения переходит в турбулентный, и нижнюю критическую скорость V_{н. к.} – при обратном переходе.

Критерием для определения режим движения жидкости является безразмерное число Рейнольдса, которое определяется по формуле:

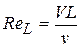, (9)

где V – средняя скорость потока, см/с; L – характерный линейный размер, см; ν – кинематический коэффициент вязкости жидкости, см²/с.

Число Рейнольдса, соответствующее нижней критической скорости V_{н. к.} называется нижним критическим числом Рейнольдса и обозначается Re_L(н.к)

Число Рейнольдса соответствующие верхней критической скорости V_{в. к.} называется верхним критическим числом Рейнольдса и обозначается Re_{L(в. к)}

^*). Дмитрий Иванович Менделеев (1834 - 1907) – выдающийся русский учёный.

^**) Осборн Рейнольдс (1842 - 1912) – английский учёный

Для напорных трубопроводов круглого сечения за характерный линейный размер L принимают диаметр трубы d, и тогда выражение для числа Рейнольдса принимается следующий вид:

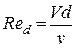, (10)

где V в см/с , d см и v в см²/с

Нижнее критическое число Рейнольдса Re_d(н.к) = 2320. Верхнее критическое число Рейнольдса Re_L(в.к) зависит от условий проведения опыта и может достигать нескольких десятков и даже сотен тысяч. Для напорных трубопроводов некруглого сечения за характерный линейный размер L принимают гидравлический радиус R, и тогда выражение для числа Рейнольдса принимает следующий вид:

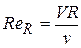, (11)

где V в см/с, R в см и v в см²/с.

Гидравлический радиус:

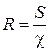, (12)

где S – площадь живого сечения потока; 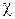– смоченный периметр.

Установим соотношение между величинами Re_d и Re_R.

Пр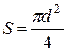и и 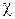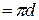гидравлический радиус 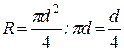, число Рейнольдса 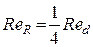и нижнее критическое число Рейнольдса .

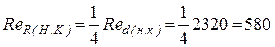Формула (11) используется также для расчёта открытых безнапорных потоков, которые наблюдаются в каналах, лотках и безнапорных трубах. Для таких потоков .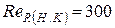

Между верхним и нижним критическими числами Рейнольдса имеется большая зона, где движение жидкости может быть как ламинарным, так и турбулентным. Практически в этой зоне режим движения жидкости считают турбулентным, так как ламинарный режим здесь очень не устойчив и легко переходит в турбулентный. Следовательно, для определения режима движения жидкости нужно найденное по формуле число Рейнольдса сравнить с его нижним критическим значением:

если 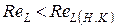, то режим движения ламинарный;

если 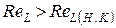, то режим движения турбулентный.