Импульс материальной точки

· Импульсомматериальнойточки массой m, движущейся со скоростью V называют векторную физическую величину, равную произведению массы точки на ее скорость:

.

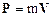Обратим внимание, что в литературе предыдущих лет широко использовался термин "количество движения", в настоящее время вместо него рекомендовано использовать термин "импульс".

Дифференцируя соотношение (2.22) по времени, получим:

.

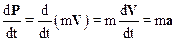Из последнего соотношения следует, что уравнение второго закона Ньютона можно записать следующим образом:

.

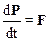Известно, что первая производная некоторой величины по времени характеризует скорость ее изменения, поэтому уравнение (2.23) читают так:

· скорость изменения импульса материальной точки равна действующей на нее силе.

Пусть на материальную точку m действует несколько постоянных сил F₁,F₂, …F_i. Обозначим равнодействующую этих сил через R:

,

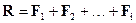и пусть Dt – время действия этих сил. Разделим этот промежуток времени на малые промежутки dt. За время dt, под действием внешних сил скорость материальной точки изменится в соответствии со вторым законом Ньютона:

.

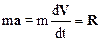Разделяя переменные в последнем соотношении 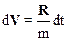, и интегрируя по времени в пределах от t1 до t2(Dt= t2- t1) , получим:

.

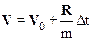Преобразуем полученное выражение к виду, определяющему изменение импульса:

.

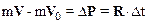В проекциях на оси координат формула (2.24) записывается так:

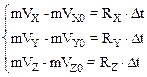
· Импульсдействия силы – векторная величина, равная произведению силы F на время ее действия Dt.

Смысл соотношения (2.24) может быть выражен следующим образом:

· приращение импульса материальной точки равно импульсу действия силы

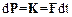или.

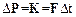Если сила F изменяется с течением времени, то импульс действия силы К равен

,

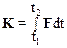где t₁ и t₂ время начала и окончания действия силы.