Получение разностных уравнений через переходные функции

Векторно-матричное описание линейного непрерывного многоканального объекта на языке дифференциальных уравнений имеет вид:

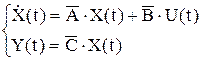
Запишем решение этого дифференциального уравнения в интегральной форме:

,

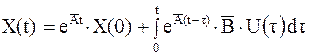где 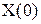- начальные условия. Значение вектора состояния для момента T имеет вид:

.

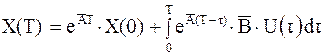Так как значение U фиксировано в течение кванта, то

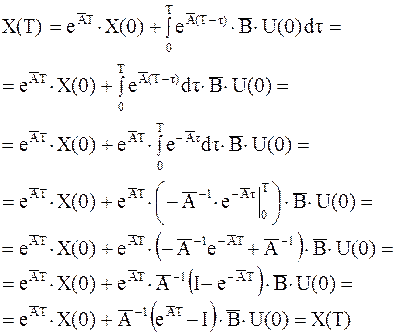
Для произвольного фиксированного момента времени вектор состояния можно найти путем сдвига аргумента. Величина шага квантования T неизменна, поэтому в окончательной записи ее опускаем:

.

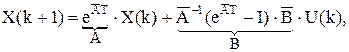
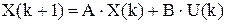В результате преобразований получены следующие соотношения:

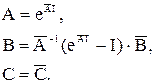
Используя разложение матричной экспоненты в ряд Фурье, матрицы можно представить в следующем виде:

(*)

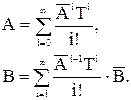Количество членов ряда необходимых для вычисления матриц A и B определяется соотношением величин коэффициентов исходных матриц и шага квантования T. В практике инженерных расчетов часто ограничиваются вычислением 3 - 4 членов ряда, что достаточно для обеспечения точности вычислений, при достаточно малом Т.