Постановка задачи

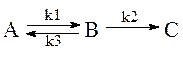Рассмотрим методику решения прямой задачи кинетики на примере системы реакций первого порядка

Заданы следующие исходные данные: k₁ = 1,5 [1/c]; k₂ = 0,5 [1/c]; k₃ = 0,1 [1/c]; C_a0 = 100 [моль/л]; C_b0 = C_c0 = 0. Для решения этой задачи потребуется математическая модель, в качестве которой могут служить дифференциальные уравнения, описывающие динамику процесса, т.е. изменения концентраций реагирующих веществ во времени.

В указанной реакции во взаимодействие вступают три вещества с текущими концентрациями C_a, C_b, C_c. Изменение концентраций этих веществ во времени записываем в виде дифференциалов dC_a/dt, dC_a/dt, dC_c/dt, которые используем в качестве левых частей дифференциальных уравнений. Правыми частями уравнений кинетики будут соотношения, записанные на основании закона действующих масс.

Рассмотрим вещество A, участвующее в двух реакциях. В первой 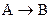концентрация вещества A убывает вследствие процесса превращения его в В. Скорость этого элементарного процесса согласно закону действующих масс представим зависимостью 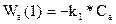, т.е. скорость пропорциональна концентрации реагирующих веществ. Знак минус показывает, что вещество A убывает.

Во второй реакции 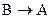вещество A пребывает в результате обратного процесса превращения вещества B в вещество A с константой k₃. Скорость этой стадии 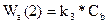, т.е. реагирующим веществом является вещество B. Знак плюс свидетельствует о том, что вещество A в реакции пребывает. Суммарная скорость по веществу A:

Учитывая, что dC_a/dt = W_a, получим новое дифференциальное уравнение кинетики по веществу А:

.

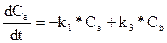По аналогии выводим следующее дифференциальное уравнение, физический смысл которого есть изменение концентрации вещества B по времени. Вещество B участвует в трех реакциях:

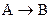(получается из A);

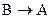(тратится на получение A);

(тратится на 1получение C).

Суммарная скорость реакции по веществу B: 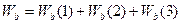, где 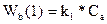, , 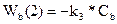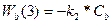. Дифференциальное уравнение кинетики по веществу.

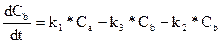
Наконец, рассмотрим скорость реакции по веществу С, которое принимает участие в одной реакции: 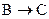. Скорость этой стадии: 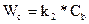, т.е. вещество С получается из В. Дифференциальное уравнение кинетики по веществу С:

.

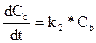В итоге, математической моделью кинетики данной системы реакций будет являться система дифференциальных уравнений

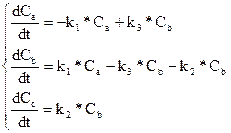
с начальными условиями при t = 0,C_a0 = 100 [моль/л], C_b0 = C_c0 = 0.

Таким образом, прямая задача кинетики (получения кривых изменения концентрации компонентов реакции во времени: C_a(t), C_b(t), C_c(t) – кинетических кривых) сводится к задаче решения системы дифференциальных уравнений с начальными условиями. Для решения этой системы на ЭВМ используя различные численные методы, например, метод Эйлера, метод Рунге – Кутта.

Воспользуемся в данном случае наиболее простым методом численного решения дифференциальных уравнений – методом Эйлера. Если имеется дифференциальное уравнение вида 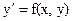с начальным условием 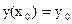, то его решение – первообразную y = y(x) – можно получить в виде дискретных точек X_k, Y_k, где 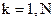- число узлов интегрирования из рекуррентных формул.

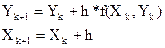
Параметр h называется шагом интегрирования, чем меньше шаг интегрирования, тем выше точность расчетов.

Предположим, что нам нужно получить кинетические кривые C_a(t), C_b(t), C_c(t) на временном отрезке от 0 до t_конца.. Возьмем шаг интегрирования h = 0,1 с, а время выдачи значений концентраций C_a, C_b, C_c на экран дисплея равным 1с (это значение принято называть шагом печати), а t_кон. Равным 20 с.

Составим блок – схему программы получения кинетических кривых (см. рис.4.1). Присвоим переменным C_a, C_b, C_c для удобства имена А, В, С. Обозначим правые части дифференциальных уравнений: первое через F1, второго через F2, третий F3.

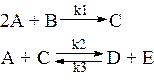Рассмотрим более сложную реакцию, протекающую по схеме

Здесь необходимо связать концентрации веществ A,B,C,D,E со степенями полноты, используя формулу (4.14).

Для данной системы реакций составляем матрицу, в который число столбов равно числу компонентов, а число строк – количеству реакций в системе. Элементами этой матрицы являются стехиометрические коэффициенты a_ij компонентов в реакции

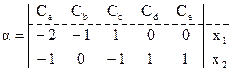
Рассмотрим первую строку матрицы , a₁=(-2,-1,1,0,0), которая показывает, что в первой реакции тратятся 2 моля вещества A? 1 моль вещества B, а вещества D и E не принимают участия в реакции (т.е. для продуктов реакции a_j > 0, для реагентов a_j < 0).

Вторая строка матрицы a₂ =(-1 0 –1 1 1) свидетельствует о том, что во второй реакции тратятся 1 моль вещества A, 1 моль вещества C и получается по одному молю веществ D и E.

Вводим степени полноты первой реакции x₁ и второй реакции x₂, тогда по уравнению (4.14) имеем

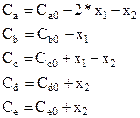
Таким образом, связь между концентрациями веществ и степенями полноты найдена в виде линейных соотношений (4.14).

Теперь переходим непосредственно к решению прямой задачи кинетики. Скорость химической реакции по определению

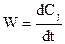
Подставляя в это соотношение вместо C_j его выражение, получаем

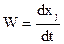или .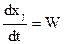

Записываем для рассматриваемой системы реакций дифференциальные уравнения кинетики. Левыми частями их будут производные по степеням полноты реакции: dx₁/dt и dx₂/dt, правые же части записываем на основании закона действующих масс.

Для реакции

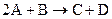
со степенью полноты x₁ дифференциальное уравнение запишется в виде

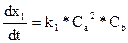
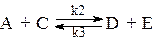Здесь скорость реакции пропорциональна концентрации реагентов A и B в степени их стехиометрических коэффициентов, а k_j является коэффициентом пропорциональности (константа скорости первой реакции).

Для второй реакции

со степенью полноты x₂ дифференциальное уравнение запишется в виде

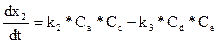
Подставляя в уравнения для степеней полноты соотношения, связывающие концентрации веществ и степеней полноты соотношения, связывающие концентрации веществ и степени полноты, получаем математическую модель кинетики неэлементарной системы реакции

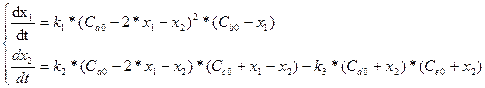
с начальными условиями: t = 0, x₁ = 0, x₂ = 0.

Решив систему дифференциальных уравнений кинетики каким – либо численным методом, получим кривые x₁(t), x₂(t). Используя связь между концентрациями компонентов и степенями полноты, можно рассчитать кинетические кривые C_a(t), C_b(t), C_c(t), C_d(t), C_e(t).