Методические указания по практической части.

В результате эксперимента, проведенного интегральным способом, получены кинетические кривые 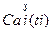, 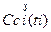(табл.5.1.). Здесь 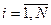, где N – количество экспериментальных точек на кинетической кривой; индекс э – относится с экспериментом.

Требуется выбрать такой механизм реакции, определить такие константы скоростей, чтобы полученные кинетические кривые (т.е. расчетные кинетические кривые) наилучшим образом описывали экспериментальные данные. Для решения поставленной задачи воспользуемся приведенной ранее последовательностью этапов.

1-й этап. – Реализован (см. табл. 5.1).

2-й этап. Если в химической реакции участвуют три компонента: A, B, C, то возможны следующие гипотезы о ее механизме:

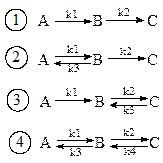
(12)

(13)

(14)

(15)

При анализе характера кривых экспериментальных зависимостей 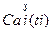, 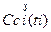в результате приведенных графических построений остановились на гипотезах (5.2) и (5.3).

3-й этап. Строим математическую модель для гипотезы (5.2):

Дифференциальные уравнения кинетики этой системы мономолекулярных реакций на основании закона действующих масс записываем в виде

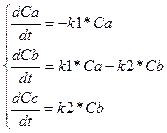
с начальными условиями t = 0, Ca = Cao, Cb = Cbo, Cc = Cco.

Математическая модель кинетики химической реакции для второй гипотезы:

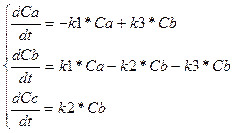
с начальными условиями t = 0, Ca = Cao, Cb = Cbo, Cc = Cco.

4-й этап. В теоретической части предложен критерий (5.1). Распишем его для наших гипотез. Здесь 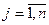, где n – число веществ, замеряемых в ходе реакции, т.е. в нашем случае n = 2 (вещества A и C); 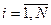, где N – число экспериментальных точек на кинетической кривой, в нашем случае N = 10. Тогда

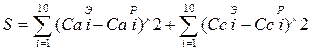(16)

Суть критерия S является сравнение в каждой точке i экспериментальных значений концентраций веществ с их расчетными значениями.

Зададимся вопросом, откуда получаются расчетные значения концентрации веществ Ca^P, Cc^P .

Совершенно очевидно, что 4-й этап – логическое продолжение 3-го этапа, т.е. полученные на 3-м этапе системы дифференциальных уравнений (5.6) и (5.7) с начальными условиями можно проигнорировать с целью получения расчетных кинетических кривых Ca^P(t), Cc^P(t) при известных значениях констант скоростей k1, k2, k3.

Таким образом, реализация этого этапа связана с принятием некоторых значений констант скоростей, входящих в дифференциальное уравнение кинетики. В нашем случае для гипотезы 1 необходимы значения двух констант k1, k2, для гипотезы 2 – значения констант k1, k2, k3.

Принимая разные значения констант скоростей, можно получить различные значения критерия адекватности S, т.е.

S1 = f ( k1,k2 ) для гипотезы 1

S2 = f ( k1, k2, k3 ) для гипотезы 2

5-й этап. Задача поиска констант отдельных стадий математически сводится к задаче поиска функции многих переменных

min S = f ( k1, k2, k3, … )

Для решения этой задачи существует несколько методов, из которых наиболее простой – метод Гаусса-Зейделя (метод поочередного изменения переменных).

Суть метода Гаусса-Зейделя состоит в следующем. Выбираем начальные значения кинетических параметров из некоторой допустимой области их определения. В нашем случае это k1h, k2h для гипотезы 1, k1h, k2h, k3h для гипотезы 2. Выбираем направления движения к минимуму критерия адекватности S для первой переменной, например k1.Для этого к значению k1h прибавляем шаг k1, т.е. k1h + D k1 и вычисляем значение критерия

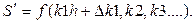
Если 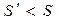, значит, направление выбрано правильно и продолжаем поиск вдоль этой переменной до тех пор, пока очередное прибавление шага D k1 не приведет к возрастанию функции S .

В случае, если 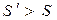направление движения надо сменить, т.е. k1h - D k1 и продолжать двигаться в избранном направлении до отыскания частного минимума.

После того как найден минимум по первой переменной k1, начинаем поиск по второй переменной k2, т.е. k2h + D k2 и вычисляем

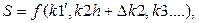
где 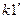- значение k1, при котором найден частный импульс S.

После отыскания минимума по второй переменной переходим к третьей переменной (для гипотезы 2).

Процесс последовательно продолжается до тех пор, пока не будет достигнута заданная точность локализации минимума: если шаг по каждой переменной приводит к возрастанию функции S, а величина шага меньше или равна заданной точности поиска.

Наконец, решив задачу поиска для гипотезы 1 (min S1) и гипотезы 2 (min S2), необходимо сделать вывод, какую из них принять. Очевидно, принимается та гипотеза, которая обеспечивает минимум критерия адекватности. Заметим, что реализация указанных процедур может быть выполнена на ЭВМ. Для этого потребуется программа расчета. Структура программы будет включать следующие разделы:

1. вод в память ЭВМ экспериментальных кинетических кривых , .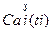

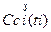2. Задание констант скоростей отдельных стадий химических реакций для выбранной гипотезы (например, задать значение k1, k2).

3. Решение системы дифференциальных уравнений кинетики численным методом Эйлера в узлах интегрирования, совпадающих с точками на экспериментальных кинетических кривых, т.е. получение Ca^P(t), Cc^P(t) (получение расчетных кинетических кривых).

4. Программирование критерия S, т.е. суммы квадратов отклонений расчетных и экспериментальных значений концентрации компонентов.

5. Печать значения критерия S.

6. Переход на выбор новых значений кинетических констант.

Блок – схема алгоритма вычисления критерия адекватности представлена на рис. 5.1.