МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОлогической ОЧИСТКИ СТОЧНЫХ ВОД в аэротенке
Биологическая очистка сточных вод нашла широкое применение в различных отраслях промышленности и городского хозяйства. Аэробные процессы биоочистки воды реализуются, как правило, в аэротенках бассейнового типа. В последние годы все большее применение находят аэротенки колонного (башенного) типа. Обеспечивая заданные показатели очистки сточных вод, они имеют значительно лучшие характеристики по эффективности массопередачи кислорода, расходу воздуха, использованию кислорода, а также требуют меньшей поверхности осветляющей емкости и общей площади производственной территории.
Вместе с тем, подавляющее большинство существующих и проектирующих аэротенков относится к бассейному типу и, естественно, остаются актуальными проблемы разработки методов интенификации этих объектов и математических моделей для целей проектирования и управления.
Известно, что структура биоценоза активного ила является чрезвычайно сложным, а обрабатываемые потоки жидкости включают много компонентные органические и неорганические примеси. Аппаратурное оформление процесса существенно осложняется наличием трех фаз: газ – жидкость – хлопья активного ила (условно твердая фаза). Эффективность актов биохимического окисления, таким образом, в значительной степени определяется гидродинамической обстановкой и массообменными характеристиками аппарата.
Учитывая пространственную распределенность процессов в аэротенке, гетерогенность биоценоза активного ила и многокомпонентность обрабатываемых потоков, можно предположить неоднородность массообменных и биохимических стадий в разных зонах аппарата в зависимости от гидродинамических режимов и состояния активного ила.
В связи с этим в данной работе предложена математическая модель переменной структуры, имеющая системно-модульный принцип построения.
Общую схему системы биоочистки сточных вод можно представить следующим образом:
 GL
GL
GG
G2X
Рис. 1. Схема системы биоочистки
Схемой предусмотрена возможность распределенного питания по субстрату и воздуху. Обобщающая стационарная модель аэротенка, учитывающая распределенность потоков:
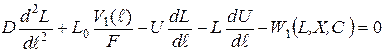 ;
;
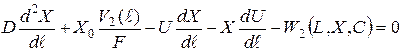 ; (1)
; (1)
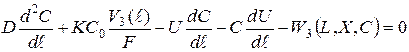
Граничные условия записываются в следующем виде:
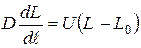 , при ℓ = 0;
, при ℓ = 0;
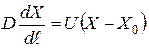 , при ℓ= 0; (2)
, при ℓ= 0; (2)
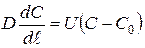 , при ℓ = 0;
, при ℓ = 0;
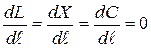 , при ℓ = ℓK.
, при ℓ = ℓK.
В системах (1) и (2) обозначены: L, X, C - текущие концентрации органических примесей, биомассы активного ила и кислорода: L0, X0, C0 - соответствующие концентрации на входе в аэротенк; V1(ℓ), V2(ℓ), V3(ℓ) - распределенные объемные скорости потоков загрязнений, биомассы и кислорода; F - площадь поперечного сечения; D - коэффициент продольного перемешивания сплошной фазы; K - расход воздуха; W1, W2, W3 - соответствующие кинетические члены; U - линейная скорость сплошного потока, отнесенная ко входу.
Таким образом, уравнения (1) соответствуют однопараметрической диффузионной модели и учитывают распределенность параметров питания. Развитием этой модели могут служить подходы, основанные на использовании более простых моделей структуры потоков (идеального вытеснения и ячеечной), а также конкретных моделей биохимической кинетики.
Следует отметить, что модель (1) не учитывает некоторые гидродинамические параметры, параметры структуры активного ила и адсорбционные эффекты на хлопьях активного ила.
Общая структура модели аэротенка может быть определена следующей схемой:

Рис.2. Структура модели аэротенка
В качестве биохимических модулей могут быть использованы модели Моно, Иерусалимского, Холдейна, Герберта и др. Алгоритмы реализации программных биохимических модулей основаны на использовании методов Рунге-Кутта и, если требуется большее быстродействие, разных модификаций метода Эйлера.
Рассмотрим массообменные модули. Наиболее часто рассматривают и учитывают в моделях массообмен по кислороду, ограничиваясь при этом массообменном в системе газ – жидкость.
Прежде всего необходимо развить модель массообмена по кислороду для трехфазной системы: газ – жидкость – хлопья активного ила. При этом можно ограничиться двумя фазовыми переходами: газ – жидкость, жидкость – хлопья, считая, что поверхность контакта газ – хлопья ничтожна мала. На массообмен по кислороду существенное влияние оказывают характеристики турбулизации среды и параметры активного ила. В зависимости от них принимается внешне-, внутри- или смешанно-диффузионный механизм кинетики массообмена.
Потребление кислорода из жидкой фазы с учетом конвективной диффузии описывается в общем случае уравнением
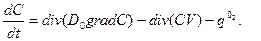 (3)
(3)
Где D0 - коэффициент продольной диффузии кислорода, V - скорость потока, q°² - интенсивность утилизации кислорода. Ясно, что при некоторых допущениях уравнение (3) переходит в форму третьего уравнения системы (1). Общий коэффициент массопередачи чаше всего считают равным коэффициенту массоотдачи из жидкой фазы: KL » bm. Однако последний измерять экспериментально довольно сложно, поэтому используют довольно объёмный коэффициент массопередачи KLQ. Для разных типов аппаратов получены различные эмпирические формулы, по которым можно оценить величину KLa. Например, для аэрируемого аппарата с перемешиванием среды формула имеет вид
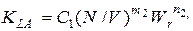 (4)
(4)
Где C1 - эмпирическая константа; N/V – удельная мощность; Wr - линейная скорость газа; m2 = 0,95; n2 = 0,67.
Можно предложить два типа массообменных модулей, соответствующих внешне-диффузионному и смешанно-диффузионному механизмам кинетики массопередачи.
1. Внешнедиффузионный механизм учитывает массопередачу газ – жидкость и жидкость – поверхность иловой частицы. Внутреннее сопротивление массопередаче частицы считается пренебрежимо малым.
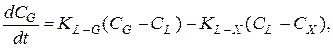 (5)
(5)
Где 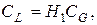
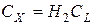 – равновесные концентрации на поверхности раздела газ – жидкость и жидкость – частица. Таким образом, в (5) мы предположили линейный характер равновесных зависимостей. Аналогично записывается уравнение (5) для CL.
– равновесные концентрации на поверхности раздела газ – жидкость и жидкость – частица. Таким образом, в (5) мы предположили линейный характер равновесных зависимостей. Аналогично записывается уравнение (5) для CL.
2. Случай смешанно-диффузионной кинетики приводит к более сложной системе уравнений.
Запишем внешнедиффузионную часть кинетического механизма в форме (5), но для CL:
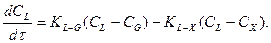 (6)
(6)
Будем считать заданной и постоянной, а CX определим как решение уравнения стационарной диффузии в сферическое зерно с последующим усреднением по объёму шара:
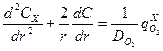 (7)
(7)
Где 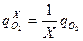 , 0 < r ≤ R, R – эквивалентный радиус иловой частицы.
, 0 < r ≤ R, R – эквивалентный радиус иловой частицы.
Для оценки величины KL-X могут быть применены две формулы в зависимости от размера иловой частицы:
-для частиц размером d<15 мкм
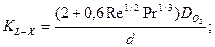 (8)
(8)
-для агломератов размером d £ 200 мкм
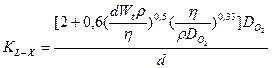 ; (9)
; (9)
где 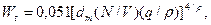 dm – диаметр, соответствующий диаметру мешалки.
dm – диаметр, соответствующий диаметру мешалки.
Рассмотрим гидродинамический модуль общей модели. В наиболее полном варианте он должен включать в себя уравнения для поля скоростей в объёме аппарата, распределения давления, газосодержания, поверхности контакта фаз и т. д. Ограничимся записью конечных соотношений, необходимых для расчета газосодержания, поверхности контакта и некоторых сопутствующих параметров:
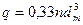
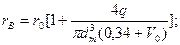
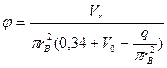 ;
; 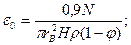 (10)
(10)
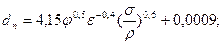
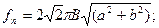
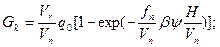
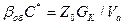
В системе (21): q – поток кислорода; n – скорость вращения мешалки; dm - диаметр мешалки; r0 - радиус мешалки; rв - расстояние, проходимое пузырем в эрлифтной струе; Vn - скорость восходящего эрлифтного течения жидкости; Vr - расход воздуха на единицу длины барботера; H , B - глубина и ширина аэротенка; j - удельное газосодержание; ε - величина диссипации энергии в единице массы перемешиваемой среды; N - мощность, рассеиваемая в зоне диспергирования; r - плотность жидкости; dn - диаметр пузыря; s - поверхностное натяжение; a и b – оси эллипсоида вращения; GK - общая скорость поглощения кислорода на единицу длины барботера; ψ- константа равновесия; b - коэффициент массопередачи; Vn - скорость подъёма пузырьков; βоб - объёмный коэффициент массопередачи; C* - равновесная концентрация; Va - рабочий объём аэротора.
К гидродинамическим модулям отнесем также систему уравнений для расчета характеристик иловых хлопьев (в частности, размер и плотность), поскольку они зависят как от биохимических, так и от гидродинамических параметров системы.
Таким образом, подготовлена структура обобщенной модели аэротенка, содержащая модули структуры потоков, биохимические модули, массообменные модули, модули гидродинамических характеристик. Для автоматизированного синтеза модули конкретного аэротенка необходимо включить в структуру обобщенной модели блок критериев и моделирующую программу. В блоке критериев задаются диапазоны изменения параметров и переменных (j, V, CL, иловые характеристики), в которых необходимо использование соответствующих модулей каждого из блоков моделей. Моделирующая программа реализует автоматизированную сборку модели той конфигурации, которая следует из сочетания получаемых критериев.
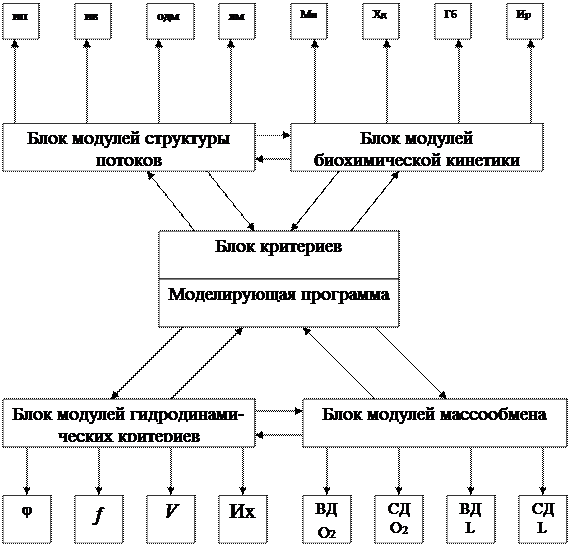 |
Рис. 3. Схема обобщенной модели переменной структуры.
Схема обобщенной модели переменной структуры приведена на рис. 3. Обозначения на схеме: ИП и ИВ – модели структуры потоков идеального перемешивания и идеального вытеснения; ОДМ – однопараметрическая диффузионная модель; КМ – комбинированные модели; биохимические модули: Мн – модель Моно, ХД – модель Холдейна, Гб – модель Герберта, Кн – модель Кенела; массообменные модули: ВД – внешнедиффузионная, СД – смешанно-диффузионная, О2- кислород, L – субстрат; гидродинамические модули: j - газосодержание, ¦ - поверхность контакта фаз, V – скоростные параметры, ИХ – иловые характеристики.
Для построения модели системы биоочистки воды в соответствии с рис.1. полученные уравнения и формулы должны быть дополнены уравнениями для отстойника и регенератора с учетом замыкания схемы.
ПРОЕКТИРОВАНИЕ АЭРОТЕНКА С РЕЦИРКУЛЯЦИЕЙ АКТИВНОГО ИЛА
Концентрация активного ила в аэротенке не может превышать величину YL0, где Y – экономический коэффициент, L0 – концентрация примесей на входе в аэротенк. Повышение концентрации активного ила возможно с помощью его рециркуляции, например, в соответствии со следующей схемой.
L¦ q(1+ r) q(1-ω) Lℓ
Аэротенк




 q Xℓ
q Xℓ
 |
q (r + ω)
q r

 x r
x r
q ω
Рис.1. Схема аэротенка с рециркуляцией активного ила.
Во вторичном отстойнике происходит отделение биомассы ила от раствора и ее уплотнение до концентрации Xr . Коэффициент рециркуляции r представляет собой отношение расхода жидкости в возвратном потоке к расходу стоков q. Время пребывания выразится следующей формулой:
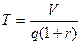 (1)
(1)
Избыточный ил удаляется из системы пропорционально доле потока v.
Систему уравнений материального баланса для аэротенка с рециркуляцией можно записать следующим образом:
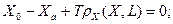 (2)
(2)
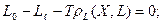
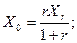 (3)
(3)
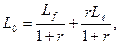
Где rх(Χ,L) и rL(Χ,L) - соответствующие выражения, описывающие биохимическую кинетику; Χ0 и L0 - концентрация ила и загрязнителя на входе в аэротенк; Lƒ - концентрация загрязнителя на входе системы.
Выражение для L0 можно упростить, имея в виду, что Lℓ << Lƒ, а r, как правило, меньше 1. При исследовании систем с рециркуляцией активного ила в качестве параметров принимают или концентрацию возвратного ила Xr , или отношение α= Xr / Xa.
Воспользовавшись моделью Моно и введя параметр α, уравнения (2) и (3) можно получить в следующем виде:
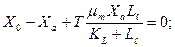 (4)
(4)
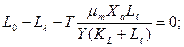 (5)
(5)
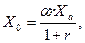
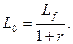 (6)
(6)
Решив систему (4) – (6) относительно Lℓ и Xa , получим
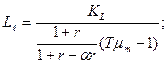 (7)
(7)
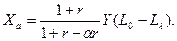 (8)
(8)
Можно ввести показатель чувствительности:
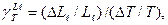
Который с учетом уравнений (7) и (8) выразится формулой
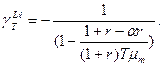 (9)
(9)
Задание. 1. составить программу для расчета концентрации и по уравнениям (7) и (8).
2.рассчитать зависимости Lℓ = Lℓ (r), Lℓ = Lℓ (α), Xa = Xa(r),
Xa = Xa (α), Lℓ = Lℓ (T), Xa = Xa (T).
3. рассчитать объём аэротенка V, обеспечивающий заданные концентрации Lℓ и Xa.
4. получить выражения, аналогичные (7) и (8) для модели кинетики Герберта при Xr = const и выполнить п.п.1-3
Исходные данные
| Вариант | KL,мг/л | Χ₀, г/л | Rн, б/в | Lн,б/р | Tн, ч | Y, гб/г.с. | L₀, мг/бак | μm, ч¯¹ |
| 0.8 | 0.7 | 0.6 | 0.1 | |||||
| 0.75 | 0.6 | 0.5 | 0.15 | |||||
| 0.6 | 0.4 | 0.6 | 0.2 | |||||
| 0.8 | 0.5 | 0.8 | 0.18 |
Дата добавления: 2015-08-01; просмотров: 3632;
