Кинетика роста популяций микроорганизмов
В процессе жизнедеятельности в организме протекает миллион ферментативных реакций. Встает задача моделирования роста организма и нахождение уравнений, описывающих скорость протекания процессов роста. Инженера интересует как растет биомасса в процессе очистке воды в аэротенке или биофильтре. Х – биомасса [г/л].
Кинетика роста популяций изучает изменение биомассы за еденицу времени (dx/dt)
Многие математические модели, описывают кинетику изменения биомассы. Одна из них (самая простая) модель Моно.
Модель Моно учитывает лимитирующее действие субстрата.
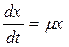 (1)
(1)
При этом Моно принял, что m – удельная скорость роста микроорганизмов подчиняется полностью закону Михалиса-Ментен:
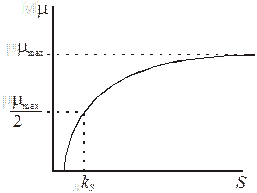
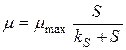 (2)
(2)
Где mmax – максимальная удельная скорость роста, S – концентрация субстрата (L – загрязнения), kS – константа полунасыщения, т.е. это такая концентрация субстрата, при которой удельная скорость роста принимает значение половины максимальной.
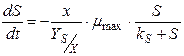 (3)
(3)
Вводиться понятие экономического коэффициента по субстратам: ys/x, который определяет какое количество субстрата пошло на прирост биомассы, на процессы жизнедеятельности и т.д. Экспериментальные исследования показывают, что микроорганизмы в самых простых случаях растут следующим образом:
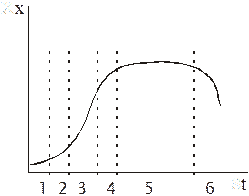 1 фаза: лакфаза (конфигурация биомассы постоянна или уменьшается, связана адаптацией);
1 фаза: лакфаза (конфигурация биомассы постоянна или уменьшается, связана адаптацией);
2 фаза: ускорения роста (культура начинает расти, после адаптации);
3 фаза: логфаза – фаза экспоненциального роста (биомасса растет по экспоненциальному закону);
4 фаза: фаза замедления роста (связана с недостаточным подводом О2 еще при наличии субстрата);
5 фаза: фаза – стационарная фаза (когда субстрат исчерпан, микроорганизмы перестают расти).
6 фаза: фаза отмирания (лизис клетки).
Другие математические модели учитывает некоторые факторы, воздействующие на биомассу.
Модель Иерусалимского. Он показал, что скорость роста биомассы максимальна при отсутствии продукта.

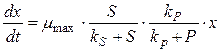 (4)
(4)
kP – константа, физический смысл которой заключается в том, что это такая концентрация продукта, при которой удельная скорость роста становится ½ от максимальной.
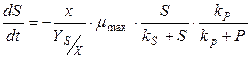 (5)
(5)
Модель Холдейна: (с учетом ингибирующего действия субстрата)
 (6)
(6)
ki – константа ингибирования.
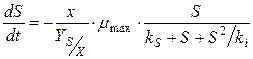 (7)
(7)
Модель Герберта (с учетом гибели микроорганизмов)
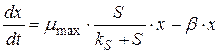 (8)
(8)
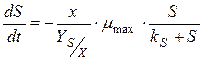 (9)
(9)
Модели для смешанных популяций учитывают гетерогенность видового состава биомассы.
Модель Кеннела (учитывает взаимоотношение микроорганизмов как хищник – жертва).
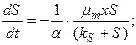 (10)
(10)
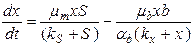 ; (11)
; (11)
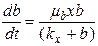 (12)
(12)
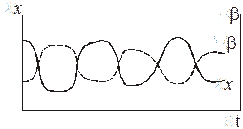 где: x – первая популяция микроорганизма (жертва), питается субстратом;
где: x – первая популяция микроорганизма (жертва), питается субстратом;
b – вторая популяция микроорганизма (хищник), питается жертвой;
S – концентрация субстрата;
mm – удельная скорость роста первого вида;
mb – удельная скорость роста второго вида;
kS – константа полунасыщения первого вида;
kx – константа полунасыщения первого вида.
Дата добавления: 2015-08-01; просмотров: 4053;
