Обратная задача кинетики

Обратная задача кинетики встречается в двух постановках:

1. Известен механизм реакции и имеются экспериментальные данные по кинетике химических реакций. Численные значения части или всех параметров реакции не известны. Требуется найти такие значения параметров реакции, чтобы полученные кинетические кривые лучшим образом аппроксимировали экспериментальные данные.

2. Имеются лишь экспериментальные кинетические кривые. Неизвестны механизм и параметры реакции. Необходимо выбрать такой механизм реакции, кинетическую модель и ее параметры, которые удовлетворяли бы эксперименту.

Как видно, оба типа обратной задачи относятся к задаче идентификации математической модели. Однако, если в первом случае идентифицируют лишь параметры кинетической модели (идентификация в узком смысле), то во втором – структуру уравнений модели и ее параметры (идентификация в широком смысле). В этой постановке обратная задача является задачей построения математической модели кинетики химических реакций.

Отметим, что из двух этих типов обратных задач наиболее часто встречается первый. Решение второй задачи обычно сводится к решению первой задачи для всех предполагаемых гипотетических механизмов. При этом выбирается тот механизм, в который отклонение расчетных данных от данных эксперимента наименьшее. Хотя более строгое обоснование выбора механизма реакции требует дополнительного анализа химической системы и проведения дополнительных экспериментов, в общем случае наличие методики решения первой задачи без применения дальнейших математических методов решить и вторую задачу.

Последовательность этапов при построении математической модели кинетики химической реакции следующая:

1. Получение экспериментальных данных.

2. Формулирование гипотезы о механизме протекания реакции.

3. Получение математической модели кинетики химической реакции.

4. Формулирование критерия адекватности модели.

5. Отыскание параметров модели кинетики химических реакций, минимизирующих критерий адекватности.

6. Принятие полученной модели или повторение пунктов 3-6

Рассмотрим содержание отдельных этапов.

1-й этап. Кинетическая модель основывается на определенных экспериментальных данных, которые должны быть тщательно спланированы. Экспериментальные данные по кинетике химических реакций получают на лабораторных установках, используя, как правило, один из основных методов постановки кинетических экспериментов – дифференциальный или интегральный. Метод называют дифференциальным, если при проведении опытов скорость реакции определяется непосредственно. Если же в ходе опытов определяется количество вещества, прореагировавшего за какой-то промежуток времени или на каком-либо участке аппарата, то метод называют интегральным, (измеряемая в эксперименте концентрация является интегралом от скорости реакции). Как интегральный, так и дифференциальный методы можно реализовать на различных аппаратах и различными методами. Для удобства дальнейшего изложения примем, что для большинства веществ системы экспериментальные данные реализованы в виде C_j = C_j(t).

2-й этап. Формулирование гипотезы о возможном механизме реакции опирается на достигнутый уровень знаний о природе и механизме химических реакций. При этом часто в механизм реакции включают лишь те элементарные стадии, в результате которых образуется устойчивый и легко идентифицируемые вещества. Такой механизм принято называть формальным (феноменологическим).

3-й этап. В соответствии со сформулированной гипотезой математическую модель кинетики обычно записывают в форме, соответствующей полученным экспериментальным данным, т.е. либо в виде зависимости скорости реакции от концентраций, либо в виде дифференциальных уравнений кинетики (см. работу № 4).

4-й этап. Сравнивают расчетные (модельные) и экспериментальные результаты. Количественная мера этого сравнения является критерием адекватности. Существуют разнообразные критерии адекватности, однако наиболее употребительным является критерий вида.

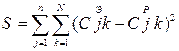(11)

где n – число веществ, по которым производится сравнение; N – количество экспериментальных точек на кинетической кривой. Индексы э и p относятся к эксперименту и расчету соответственно.

5-й этап. Для решения задачи минимизации функции многих переменных предложено значительное количество методов. Сравнение их не позволяет априори утверждать, что какой-то метод заведомо лучше другого. При выборе подходящего метода для решения конкретной задачи необходимо учитывать такие факторы, как характер минимизируемой функции, точность предварительной оценки параметров, общее число переменных, по которым производится сравнение, и т.д. При этом не следует забывать, что ресурсы ЭВМ ограничены.