Спецификация модели.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Она включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы).
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
3. Включаемые факторы не должны коррелировать друг с другом. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т. е. имеет место совокупное воздействие факторов друг на друга. Одним из индикаторов определения наличия мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8 (rxi xj) и др.
При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия.
Практика построения многофакторных моделей взаимосвязи показывает, что все реально существующие зависимости между социально экономическими явлениями можно описать используя пять типов моделей:
1) Линейная:
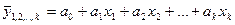
2) Степенная
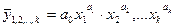
3) Показательная
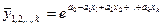
4) Параболическая
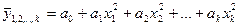
5) Гиперболическая
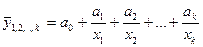
Наиболее приемлемым способом определения вида исходного уравнения регрессии является метод перебора различных уравнений.
Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные формы зависимости приводятся к линейным путем линеаризации. В линейной множественной регрессии 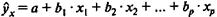 параметры при xназываются коэффициентами «чистой» регрессии.Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
параметры при xназываются коэффициентами «чистой» регрессии.Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.
Уравнение множественной регрессии можно построить в естественном и стандартизированном виде.
А) Построение уравнения в естественном виде. Так, для уравнения у = а + b1 · х1 + b2 · х2 + ··· + bр · хр + ε система нормальных уравнений составит:
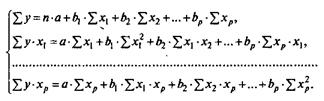
Ее решение может быть осуществлено методом определителей:
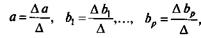
где Δ — определитель системы;
Δа, Δb1,..., Δbp — частные определители.
Б) Возможен и иной подход к определению параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:
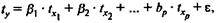
где 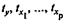 — стандартизованные переменные:
— стандартизованные переменные: 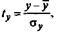
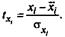
для которых среднее значение равно нулю:
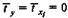
а среднее квадратическое отклонение равно единице:
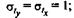 β -стандартизованные коэффициенты регрессии.
β -стандартизованные коэффициенты регрессии.
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида

Решая ее методом определителей, найдем параметры — стандартизованные коэффициенты регрессии (β-коэффициенты).
Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор xj, изменится на одну сигму при неизменном среднем уровне других факторов. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат.
От уравнения в стандартизированном виде можно перейти к уравнению в естественной форме. Так, переход для двухфакторного уравнения множественной регрессии можно записать следующим образом:
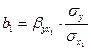
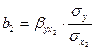
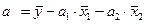
Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата - коэффициента детерминации.
Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
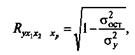
где σ2у — общая дисперсия результативного признака;
σ2ост - остаточная дисперсия для уравнения y =f(x1 , x2,..., xp).
Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:
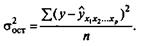
При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:
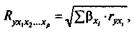
где βxi - стандартизованные коэффициенты регрессии;
rуxi -парные коэффициенты корреляции результата с каждым фактором.
Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы:
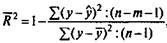
где т - число параметров при переменных х;
n - число наблюдений.
Поскольку 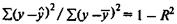 , то величину скорректированного индекса детерминации можно представить в виде
, то величину скорректированного индекса детерминации можно представить в виде
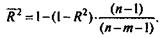
Чем больше величина m, тем сильнее различия 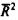 и R2.
и R2.
Парные коэффициенты корреляции.Для измерения тесноты связи между двумя из рассматриваемых переменных(без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.
Частные коэффициенты корреляции. Однако в реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень влияния одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества переменных, влияние которых исключается (элиминируется), частные коэффициенты корреляции могут быть различного порядка. При исключении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключении влияния двух переменных – второго порядка и т.д. Парный коэффициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.
Частный коэффициент корреляции первого порядка между признаками у и х1 при исключенном влиянии признака х2 вычисляется по формуле
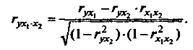
где r – парные коэффициенты корреляции между соответствующими признаками.
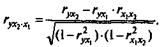
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так по уравнению
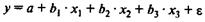
возможно исчисление трех частных коэффициентов корреляции второго порядка:
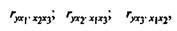
каждый из которых определяется по рекуррентной формуле. Например, при i = 1 имеем формулу для расчета ryx1*x2x3 , а именно
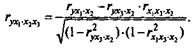
В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения. В основном их используют на стадии формирования модели, в частности в процедуре отсева факторов.
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:
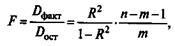
где Dфакт - факторная сумма квадратов на одну степень свободы;
Dост - остаточная сумма квадратов на одну степень свободы;
R2- коэффициент (индекс) множественной детерминации;
т - число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов);
n- число наблюдений.
Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный F-критерий, т. е. Fxj.
Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что оцениваем значимость влияния x1 как дополнительно включенного в модель фактора. Используем следующую формулу:
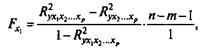
где R2yx1x2...xp - коэффициент множественной детерминации для модели с полным набором факторов;
R2yx2....xp ~ тот же показатель, но без включения в модель фактора x1;
n- число наблюдений;
т - число параметров в модели (без свободного члена).
Фактическое значение частного F-критерия сравнивается с табличным при 5%-ном или 1%-ном уровне значимости и числе степеней свободы: 1 и n— т — 1. Если фактическое значение Fxj. превышает 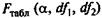 , то дополнительное включение фактора xj в модель статистически оправданно и коэффициент чистой регрессии bi при факторе xi- статистически значим. Если же фактическое значение Fxj меньше табличного, то дополнительное включение в модель фактора х, не увеличивает существенно долю объясненной вариации признака у, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.
, то дополнительное включение фактора xj в модель статистически оправданно и коэффициент чистой регрессии bi при факторе xi- статистически значим. Если же фактическое значение Fxj меньше табличного, то дополнительное включение в модель фактора х, не увеличивает существенно долю объясненной вариации признака у, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.
С помощью частного F-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор xi- вводился в уравнение множественной регрессии последним.
Дата добавления: 2015-08-01; просмотров: 991;
