Нелинейная регрессия.
Различают два класса нелинейных регрессий:
• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. К этому классу относятся полиномы различных степеней, равносторонняя гипербола. Параметры определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам.
• регрессии, нелинейные по оцениваемым параметрам. К этому классу относятся следующие функции: степенная, показательная, экспоненциальная и др.
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции (R):
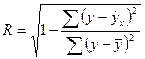
Величина данного показателя находится в границах: 0 ≤ R ≤ 1, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации.
Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции.
Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:
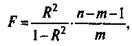
где R2 - индекс детерминации;
n - число наблюдений;
т — число параметров при переменных х.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую.
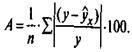
Ошибка аппроксимации в пределах 5—7 % свидетельствует о хорошем подборе модели к исходным данным.
Дата добавления: 2015-08-01; просмотров: 1081;
