Потік векторного поля

Коли визнати, що векторне поле 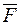є швидкість рідини, яка протікає через поверхню s, то цей добуток дорівнює кількості рідини, яка протікає через площинку 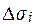за одиницю часу в напрямку вектора .
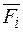Вираз 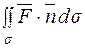являє собою загальну кількість рідини, що протікає за одиницю часу через поверхню s.

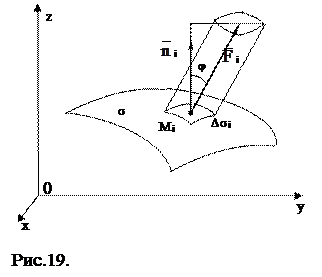
Таким чином, поверхневий інтеграл 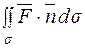зветься потоком векторного поля 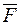через поверхню s.

Якщо розкрити скалярний добуток, то одержимо:

.

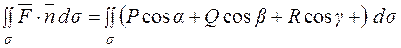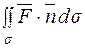Векторне поле можна розглядати як суму трьох векторних полів, тоді і інтеграл також можна виразити через суму трьох інтегралів:

.

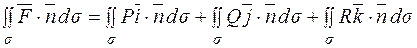Розглянемо останній з інтегралів: 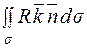. 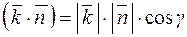(рис.20). Далі: 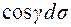є проекція площинки ds на площину XOY: 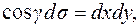то можна записати: .

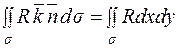Аналогічно: .

Весь інтеграл записується так:

.

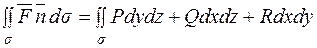Відповідно до запису цей поверхневий інтеграл другого роду ще звуть поверхневим інтегралом по координатах.

Зауважимо, що в запису 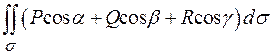в дужках є скалярна функція. Позначивши її через u(x;y;z)=P(x;y;z)cosa+Q(x;y;z)cosb+R(x;y;z)cos 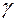, маємо 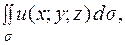тобто поверхневий інтеграл першого роду.

Таким чином, рівність 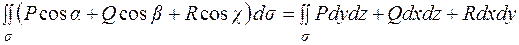відображає, по суті, зв'язок між поверхневими інтегралами першого та другого роду.