Описание векторного способа задания движения
Из определения 3 (п.3º §4 Введения) вытекает, что для того, чтобы задать движение материальной точки, необходимо:
1) выбрать точку отсчета (обозначим ее 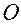 ),
),
2) задать вектор-функцию 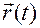 на том промежутке времени, где хотим знать о движении, причем вектор-функция должна быть дважды непрерывно дифференцируема по
на том промежутке времени, где хотим знать о движении, причем вектор-функция должна быть дважды непрерывно дифференцируема по 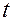 ,
,
3) задать положение точки в момент времени 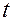 относительно точки отсчета равенством
относительно точки отсчета равенством
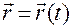 , (1.1.1)
, (1.1.1)
где
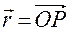 — радиус-вектор той геометрической точки абсолютного пространства, с которой в момент времени
— радиус-вектор той геометрической точки абсолютного пространства, с которой в момент времени 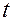 по своему положению совпадает материальная точка
по своему положению совпадает материальная точка 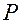 .
.
Таким образом, на равенство (1.1.1) можем смотреть, как на способ задания движения материальной точки. Такой способ называется векторным заданием движения точки.
1.2. Вычисление скорости и ускорения при векторном
способе задания движения
Из (1.1.1) согласно определениям скорости и ускорения вытекает, что скорость и ускорение точки при известном ее движении 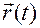 вычисляются по формулам
вычисляются по формулам
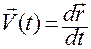 ,
, 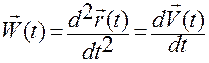 . (1.1.2)
. (1.1.2)
Заметим, что векторы 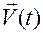 и
и 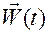 , задаваемые формулами (1.1.2), имеют своим началом геометрическую точку
, задаваемые формулами (1.1.2), имеют своим началом геометрическую точку 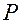 , которая служит концом радиус-вектора
, которая служит концом радиус-вектора 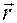 , устанавливающего положение материальной точки в момент времени
, устанавливающего положение материальной точки в момент времени 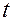 .
.
Дата добавления: 2015-08-21; просмотров: 811;
