Примечание 1. Если известна скорость , то, как следует из сказанного, движение определяется из уравнения (1.1.3):

Если известна скорость 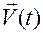, то, как следует из сказанного, движение определяется из уравнения (1.1.3):

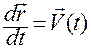. (1.1.3)

посредством вычисления интеграла от вектора скорости.

В уравнение (1.1.3) движение входит через свою производную по времени.

Равенство, в которое входят производные от неизвестной функции, зависящей от одного аргумента, называется обыкновенным дифференциальным уравнением.

Порядком уравнения называют наивысший порядок производной от неизвестной функции, с которым эта функция входит в данное уравнение. При этом сама функция может входить или не входить в уравнение.

Как видим, уравнение (1.1.3)

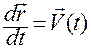(1.1.3)

является дифференциальным уравнением первого порядка относительно вектор-функции 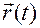, а уравнение (1.1.6):

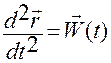(1.1.6)

— дифференциальным уравнением второго порядка.

Функция, дифференцируемая в количестве раз, совпадающем с порядком дифференциального уравнения, и обращающая это уравнение в тождество относительно независимой переменной, называется решением данного дифференциального уравнения.

Согласно этому определению, вектор-функция 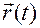, задаваемая формулами (1.1.5)и (1.1.9), является решением уравнения (1.1.3) и (1.1.6), соответственно.

Таким образом, если движение точки определять через скорость или ускорение, то оно строится как решение векторного обыкновенного дифференциального уравнения.

В таких случаях дифференциальное уравнение, решением которого является закон движения материальной точки, называется математической моделью ее движения.