Построение движения точки по заданному ее ускорению
Пусть теперь известно ускорение 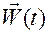 в любой момент времени
в любой момент времени 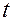 из промежутка, на котором должно быть определено движение.
из промежутка, на котором должно быть определено движение.
Движение связано с ускорением следующим соотношением:
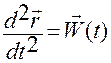 . (1.1.6)
. (1.1.6)
Если учесть, что скорость 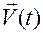 связана с ускорением
связана с ускорением 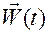 (по определению) соотношением
(по определению) соотношением
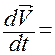
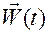 , (1.1.7)
, (1.1.7)
то из (1.1.7) можем определить скорость 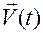 по известному вектору
по известному вектору 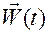 .
.
Для этого воспользуемся формулой (1.1.5)
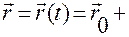
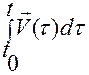 , (1.1.5)
, (1.1.5)
в которой 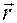 ,
, 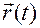 ,
, 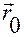 ,
, 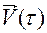 заменим соответственно на
заменим соответственно на 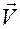 ,
, 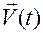 ,
, 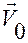 ,
, 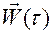 ;
;
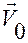 обозначает вектор скорости, которую имеет материальная точка в момент времени
обозначает вектор скорости, которую имеет материальная точка в момент времени 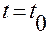 .
.
Получим
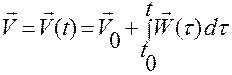 . (1.1.8)
. (1.1.8)
Учитывая связь (1.1.3):
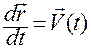 (1.1.3)
(1.1.3)
скорости 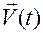 с движением
с движением 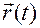 , подставим найденную функцию
, подставим найденную функцию 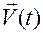 в (1.1.5):
в (1.1.5):
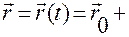
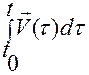 . (1.1.5)
. (1.1.5)
В результате получим вектор-функцию 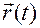 , определяющую такое движение материальной точки, при котором она имеет ускорение, совпадающее в каждый момент времени
, определяющую такое движение материальной точки, при котором она имеет ускорение, совпадающее в каждый момент времени 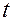 с заданным ускорением
с заданным ускорением 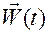 :
:
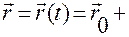
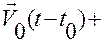
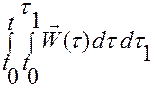 . (1.1.9)
. (1.1.9)
На этом движении материальная точка в момент времени 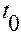 проходит через положение
проходит через положение 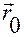 и имеет в нем скорость
и имеет в нем скорость 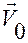 .
.
Из (1.1.9) следует, что для однозначного построения движения материальной точки по ускорению 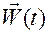 требуется задать не только положение
требуется задать не только положение 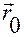 в момент
в момент 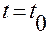 , но и скорость
, но и скорость 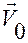 .
.
Дата добавления: 2015-08-21; просмотров: 695;
