Построение движения по заданной скорости

Соотношение (1.1.1):

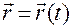, (1.1.1)

— это векторный способ задания движения, позволяющий определить положение точки 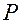в любой момент времени .

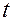Соотношение (1.1.2):

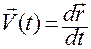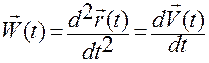, . (1.1.2)

— это способ вычисления недостающих кинематических характеристик в этот момент (скорости и ускорения материальной точки) по заданному движению.

Однако движение может быть определено и в том случае, когда задана скорость или ускорение материальной точки на том промежутке времени, на котором необходимо знать о движении.

Действительно, если в любой момент времени 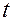задана скорость 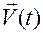, то имеем

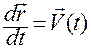. (1.1.3)

Справа стоит известная вектор-функция 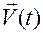. Слева — вектор-функция 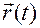, определяющая движение точки, является неизвестной.

На формулу (1.1.3) можем смотреть, как на уравнение для определения движения.

Из него следует, что 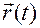является первообразной для функции 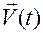, а потому

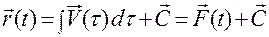. (1.1.4)

Здесь 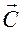— некоторый постоянный вектор, а 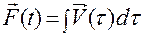— первообразная функция вектор-функции .

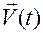Соотношение (1.1.4) задает семейство движений, каждое из которых имеет в любой момент времени 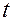заданную скорость .

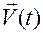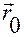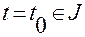Чтобы из формулы (1.1.4) выделить конкретное движение, проходящее через заданную геометрическую точку с радиус-вектором при , надо положить в (1.1.4) слева 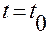и .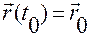

Тогда получим

,

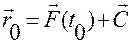где 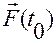— значение первообразной 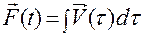в момент .

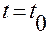Выразив отсюда 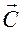, найдем

.

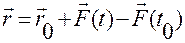Поскольку

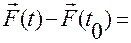
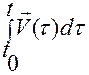
— это определенный интеграл от векторной функции 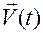, то можем записать

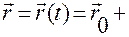
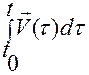. (1.1.5)

Формула (1.1.5) – это векторная форма определения движения точки при задании ее скорости 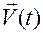как функции времени.