Застосування оператора Гамільтона до добутку скалярних та векторних полів

При вживанні оператора набла до добутку двох полів, якими можуть бути 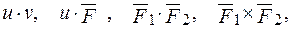треба користуватися правилами векторної алгебри та правилами диференціювання.

Як диференціальний оператор він діє лише на множник, що стоїть безпосередньо за ним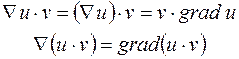

В останньому випадку за правилами диференціювання .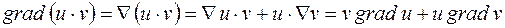

Як бачимо, у процесі диференціювання на певному етапі ми деякі функції вважаємо фіксованими (сталими). Щоб виділити ці функції, їх позначають індексом, наприклад:

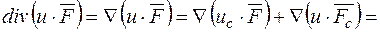
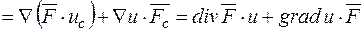
До речі, цей же результат можна одержати без вживання оператора набла:

.

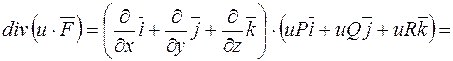
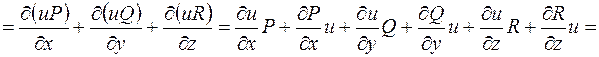
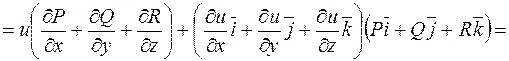
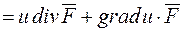Ще приклад:

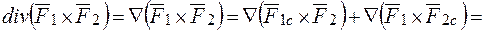далі, користуючись циклічністю мішаного добутку трьох векторів 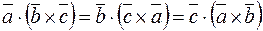, запишемо останній вираз так, аби оператор набла стояв безпосередньо перед тією функцією, на яку він діє:

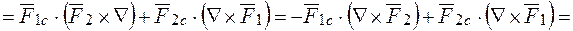
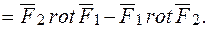
Введений індекс є допоміжним і в кінці обчислення його не пишуть, наприклад,

.

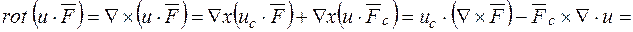
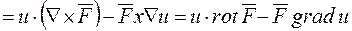Ми розглянули деякі диференціальні операції першого порядку. Після їх застосування до поля виникає нове поле, до якого знову можна вжити ці операції У результаті маємо диференціальні операції другого порядку. Таких операцій існує лише п'ять:

у скалярному полі u=u(x,y,z)

Ñ×(Ñu)=ÑÑu = div grad u

Ñ´(Ñu)=Ñ´Ñu = rot grad u

у векторному полі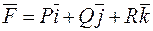

.

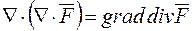
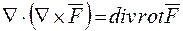
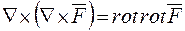Розглянемо ці операції докладніше:

.

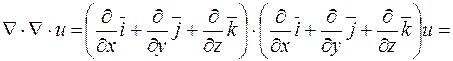
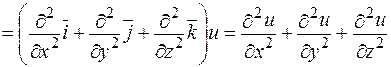Оператор Ñ×Ñ позначається через D ("дельта") і зветься оператором Лапласа.

Отже, 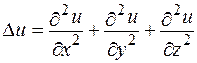або Du=div grad u (як відомо, векторний добуток 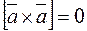). Це означає, що поле градієнта є безвихорним. Зокрема, в електротехніці ,

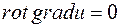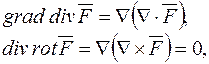
оскільки в мішаному добутку векторів є два однакових вектори.

Це значить, що поле вихору – поле соленоїдальне

,

тут 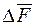‑ результат застосування оператора Лапласа до вектора 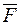, а до подвійного векторного добутку застосовано перетворення .